Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

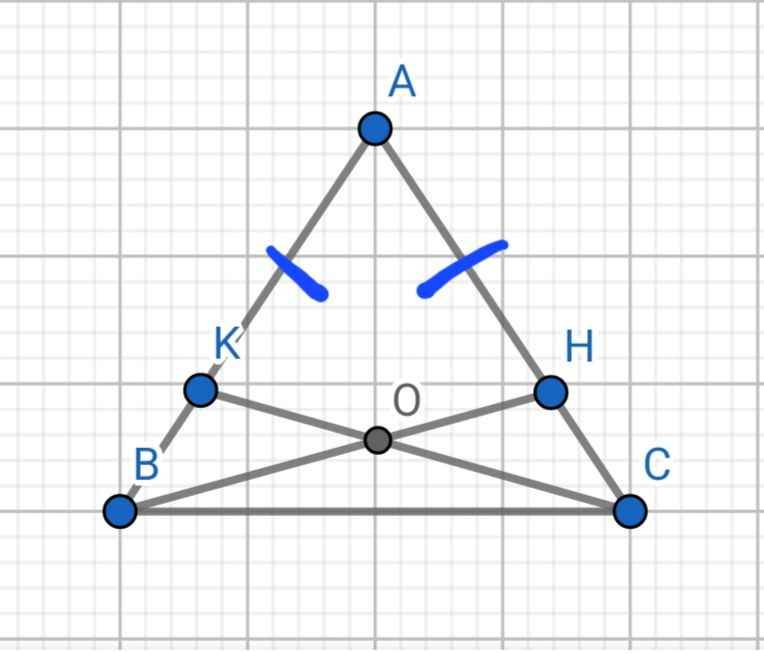
Do ∆ABC cân tại A
⇒ AB = AC và ∠ABC = ∠ACB
AK = AH
⇒ BK = CH
Xét ∆BHC và ∆CKB có:
CH = BK (cmt)
∠BCH = ∠CBK (∠ACB = ∠ABC)
BC chung
⇒ ∆BHC = ∆CKB (c-g-c)
⇒ ∠HBC = ∠KCB (hai góc tương ứng)
∠OBC = ∠OCB
∆OBC có ∠OBC = ∠OCB
⇒ ∆OBC cân tại O

Vì tam giác ABC cân tại A
=> Góc ABC=ACB
=> AB=AC ( t/c tam giác cân) (1)
Mà AH=AK ( gt) (2)
Và AH+HC=AC; AK+KB=AB (3)
Từ (1)(2)(3) => HC = KB
Xét tam giác KBC và HCB có:
BC chung
Góc ABC=ACB ( chứng minh trên)
KB=HC ( chứng minh trên)
=> Tam giác KBC=HCB ( c.g.c )
=> Góc KCB=HBC
Hay tam giác OBC cân tại O
xin loi minh ko biet nha bn
xin loi minh ko biet nha bn
xin loi minh ko biet nha bn

Xét tam giác ABH và ACK có:
AH=AK(gt)
AB=AC(tam giác ABC cân)
Â:góc chung
=> ABH=ACK
=> Góc ABH= Góc ACK
=> Góc OBC= Góc OCB
=> OBC cân tại O
Ta có tam giác ABC là tam giác cân tại A AB=AC; B=C (tính chất tam giác cân) Xét tam giác ACK và tam giác ABH có: AK=AH(giả thiết) A chung AC=AB(giả thiết) => tam giác ACK=tam giác ABH(c.g.c) OBC=OCB(2 góc tương ứng) Ta có B=OBC + KBO C=OCB + HCO Mà B=C(giả thiết) KBO= HCO(cmt) => OBC= OCB => OBC là tam giác cân

Bạn tự vẽ hình nha!!
a, Phần a cứ sai sai sao ấy nên mk ko lm đc
b, Xét tam giác AOC và tam giác BOC có:
OA=OB(GT)
Góc AOC= góc BOC( tia Ot là tia pg của góc O)
OC chung
=>Tam giác AOC= tam giác BOC(c.g.c)
=>AC=BC( 2 cạch tương ứng)
=>Tam giác ABC cân ở A(đpcm)
c, Xét tam giác HOC và tam giác KOC có:
Góc OHC = góc OBC =90'( CH vuông góc Ox, CK vuông góc Oy)
OC chung
Góc HOC = góc BOC(GT)
=>Tam giác HOC= tam giác KOC(ch-gn)
=>OH=OB(2 cạnh tương ứng)
=>Tam giác OHK vuông tại O

Xét ΔHBC và ΔKCB có
HC=KB
\(\widehat{HCB}=\widehat{KBC}\)
BC chung
Do đó: ΔHBC=ΔKCB
Suy ra: \(\widehat{HBC}=\widehat{KCB}\)
=>\(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O

2 cách
Cách 1
Do tam giác ABC cân tại A nên góc ABC=góc ACB và AB=AC
Do AB=AC mà AK=AH=> KB=HC
Xét tam giác BKC và tam giác CHB có:
-BK=HC -góc ABC=góc ACB -BC chung
=> tam giác BHC=tam giác CKB(c.g.c)
=>góc CHB=góc BKC
Xét tam giác KOB và tam giác HOC
-góc BKO=góc CHO
-BK=HK
-góc KOB=góc HOC
=>.tam giác KOB=tam giác HOC (g.c.g)
=>BO=CO ( chôc này bn có thể nói góc bằng nhau rồi cộng góc lại cx đc)
=> tam giác BOC cân tại O ( đpcm)
Cách 2
Xét tam giác ABH và tam giác ACK có
-AK=AH
-góc A chung
-AB=AC( tam giác ABC cân tại A)
=>góc ABH=góc ACB
=>góc HBC=góc KCB
=> tam giác OBC cân tại O ( Đpcm)
Vì tam giác ABC cân tại A, nên ta có AB = AC.
Với AK = AH và AB = AC, ta có tam giác AKH cân tại A.
Gọi M là trung điểm của KH, ta có AM song song với BC và AM = 1/2 BC.
Ta thấy rằng tam giác BOM và COM đều có cạnh ON (với N là trung điểm BC), BM = MC và góc BOM = 180° - góc COM.
Như vậy, tam giác BOC cân tại O vì OB = OC (cùng là đường trung bình trong tam giác đều BOC) và góc BOC = 2 × góc BOM = 2× (90° – 1/2 × góc MBC) = 180° – góc MBC = góc BOC (vì tam giác BOC cân tại O).