Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \(\Delta ABH\)và \(\Delta ACH\)có:
\(AB=AC\)(gt)
\(\widehat{ABH}=\widehat{ACH}\)(gt)
\(BH=CH\)(gt)
suy ra: \(\Delta ABH=\Delta ACH\)(c.g.c)

Câu a: Chứng minh tam giác ABH = tam giác ACH
Ta có tam giác ABC cân tại A, tức là ( AB = AC ).
Điểm ( H ) là trung điểm của đoạn ( BC ), nên ( BH = HC ).
Xét hai tam giác ( ABH ) và ( ACH ):
- ( AB = AC ) (giả thiết tam giác ABC cân tại A).
- ( BH = HC ) (do ( H ) là trung điểm của ( BC )).
- ( \angle ABH = \angle ACH ) (đối đỉnh).
Vậy theo cạnh - góc - cạnh (c.g.c), ta có:
[ \triangle ABH = \triangle ACH ]
Câu b: Chứng minh ( \angle ABM = \angle ACM ) và tam giác MBC cân
- Vì ( M ) nằm trên tia phân giác của góc ( ABC ), ta có: [ \angle ABM = \angle CBM ]
- Mặt khác, do tam giác ( ABH ) và ( ACH ) bằng nhau (chứng minh ở câu a), nên: [ \angle CBM = \angle ACM ] Suy ra:
[ \angle ABM = \angle ACM ] - Xét tam giác ( MBC ):
- ( \angle CBM = \angle BCM ) (do ( M ) nằm trên tia phân giác của ( \angle ABC )).
- ( MB = MC ) (cạnh đối diện hai góc bằng nhau).
Vậy tam giác ( MBC ) cân tại ( M ).
Câu c: Chứng minh ( AB = AN )
- Do đường thẳng đi qua ( A ) song song với ( BC ) cắt tia ( BM ) tại ( N ), ta có:
[ AN \parallel BC ] - Xét tam giác ( ABN ), có ( AN \parallel BC ) nên theo định lý đường trung bình của tam giác, ta có:
[ AB = AN ]
Câu d: Chứng minh ( MC \perp CN )
- Từ câu b, tam giác ( MBC ) cân tại ( M ) nên ( MC = MB ).
- Do ( AN \parallel BC ), nên góc ( MCN ) bằng góc ( NBC ).
- Mà ( \angle NBC = 90^\circ ) (do đường thẳng ( AN ) song song với ( BC )).
- Vậy suy ra ( MC \perp CN ).

a: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là phân giác của góc BAC
c: ΔABC cân tại A
mà AH là trung tuyến
nên AH là trung trực của BC
=>I nằm trên trung trực của BC
=>IB=IC
d: Xet ΔABN có góc ABN=góc ANB=góc MBC
nên ΔABN can tại A
=>AB=AN
e: Xét ΔABC co
BM,AM là phân giác
nên M là tâm đừog tròn nội tiếp
=>CM là phân giác của góc ACB
Xét ΔHCM vuông tại H và ΔKCM vuông tại K có
CM chung
góc HCM=góc KCM
=>ΔHCM=ΔKCM
=>MH=MK





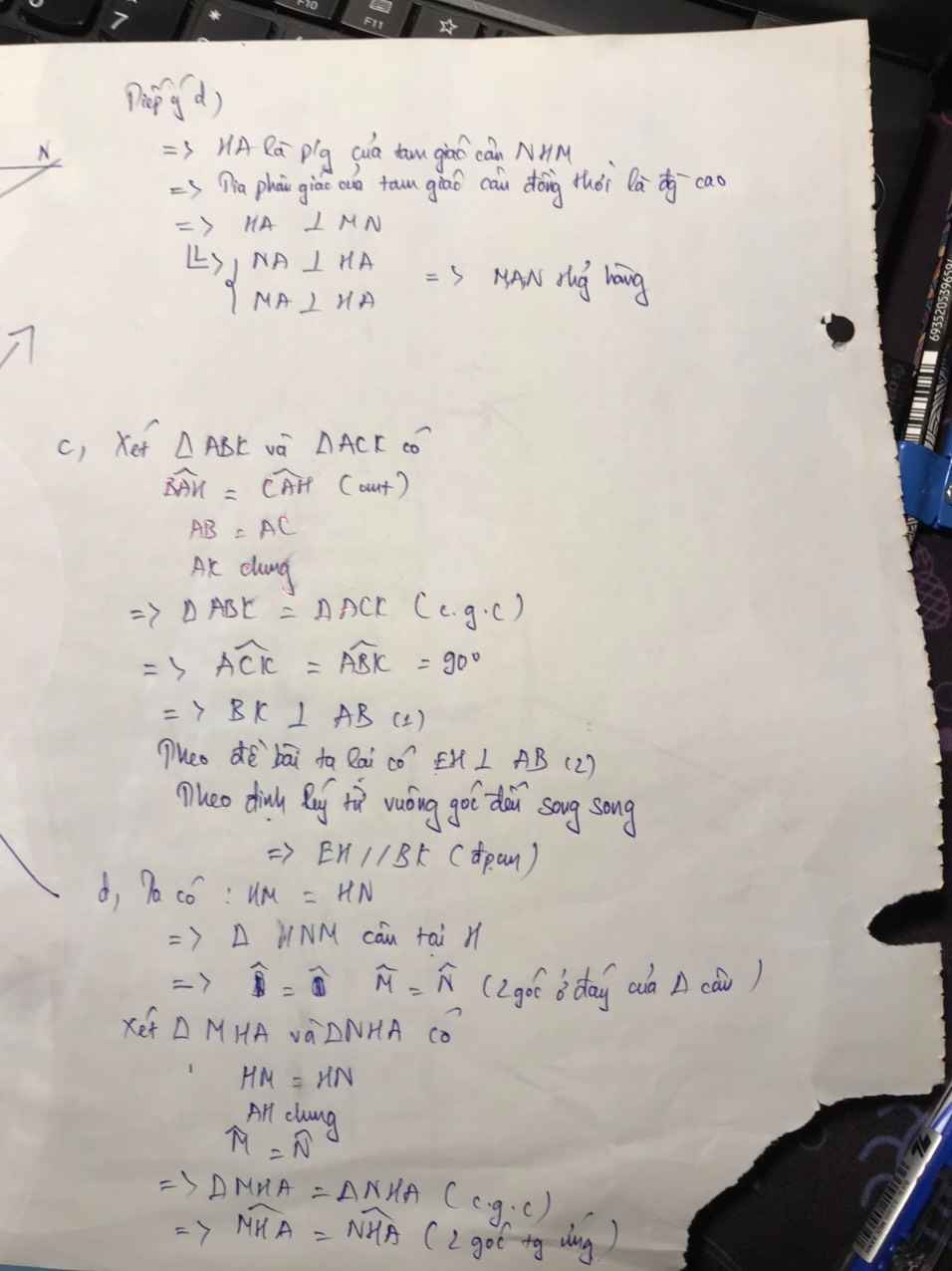


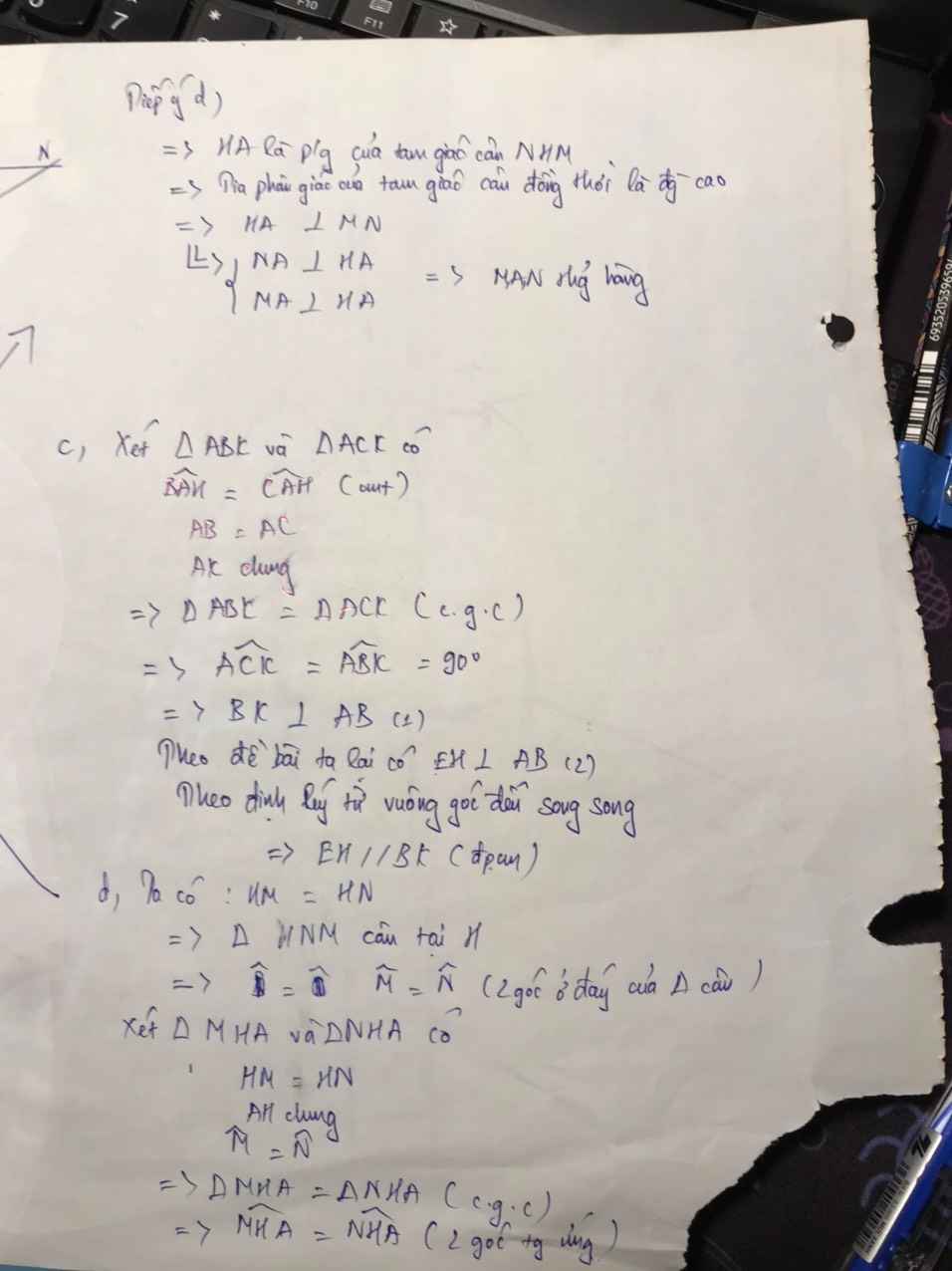


a/ Xét T/g ABH và T/g ACH ta có :
+ AB = AC ( T/g ABC cân tại A )
+ BH = CH ( H là trung điểm BC )
+ Góc ABH = ACH ( T/g ABC cân tại A )
=> T/g ABH = T/g ACH (C.g.c)
b/Xét T/g ABM và T/g ACM ta có
+ Ab = Ac ( T/g ABC cân tại A )
+ AM chung
+ BAM = CAM ( T/g ABH = T/g ACH )
=> T/g ABM = T/g ACM (C.g.c)
- Ta có :
BM = CM ( T/g ABM = T/g ACM)
=> T/g MBC cân tại M