Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tự kẻ hình nha
a) - Vì tam giác ABC cân tại A (gt)
=> AB = AC (định nghĩa)
góc ABC = góc ACB (dấu hiệu)
- Vì AH vuông góc với BC (gt)
=> tam giác ABH vuông tại H (tc)
tam giác ACH vuông tại H (tc)
- Xét tam giác vuông ABH và tam giác vuông ACH, có:
+ AB = AC (cmt)
+ Chung AC
=> tam giác vuông ABH = tam giác vuông ACH (cạnh huyền - cạnh góc vuông)
b) - Vì tam giác vuông ABH = tam giác vuông ACH (cmt)
=> BH = CH (2 cạnh tương ứng)
=> AH là đường trung tuyến tam giác ABC (dấu hiệu)
- Vì N là trung điểm của AC (gt)
=> BN là đường trung tuyến tam giác ABC (dấu hiệu)
Mà G là giao điểm của BN và AH (gt)
=> G là trọng tâm của tam giác ABC (tc)
- Xét tam giác ANG và tam giác CNK, có:
+ NG = NK (gt)
+ AN = CN (N là trung điểm của AC)
+ góc ANG = góc CNG (đối đỉnh)
=> tam giác ANG và tam giác CNK (cgc)
=> góc AGN = góc CKN (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
=> AG // CK (dấu hiệu)
c) - Vì G là trọng tâm của tam giác ABC (cmt)
=> BG = 2/3 BN (tc)
=> NG = 1/3 BN
Mà NK = NG (gt)
=> NK = 1/3 BN
=> NK + NG = 1/3 BN + 1/3 BN
=> GK = 2/3 BN
Mà BG = 2/3 BN (cmt)
=> GK = BG
=> G là trung điểm BK

Xét tg ABC có; AH là trung tuyến cạnh BC; BN là trung tuyến của cạnh AC
Mà AH và BN cắt nhau tại G => G là trọng tâm
=> CG là trung tuyến cạnh AB hay CM là trung tuyến canh AB (do M là trung điểm cạnh AB)
=> \(AG=\frac{2}{3}AH;GH=\frac{1}{3}AH;CG=\frac{2}{3}CM;GM=\frac{1}{3}CM\)
Ta có: \(BC+AG=2HC+\frac{2}{3}AH=2\left(CH+\frac{1}{3}AH\right)\)
\(=2\left(CH+GH\right)>2CG\) (BĐT tam giác)
\(=2\cdot\frac{2}{3}CM=\frac{4}{3}CM=4GM\) (dpdcm)

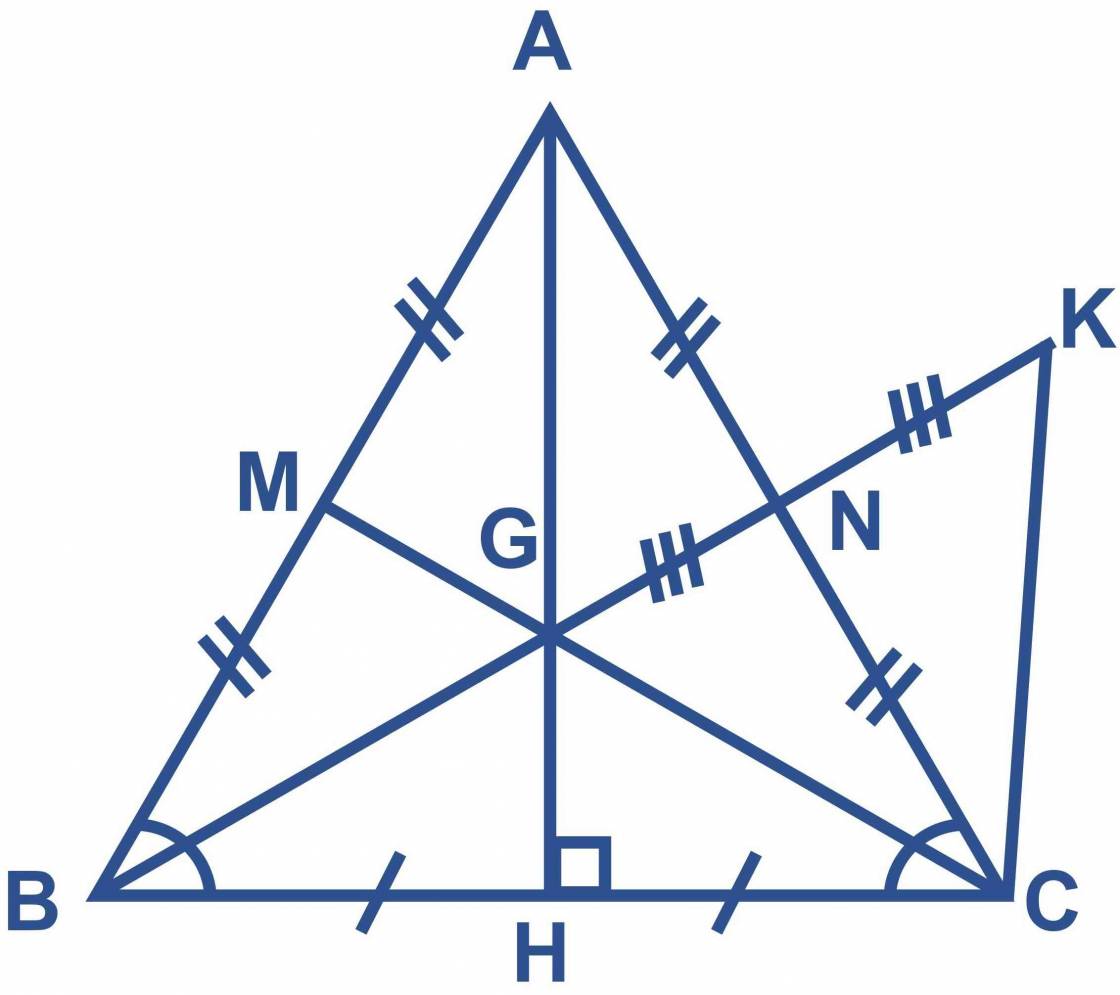
a) trong ΔABC, có góc AHB là góc vuông
góc ABH là góc nhọn
⇒ góc AHB > góc ABH
⇒ AB > AH
b) M là trung điểm của AB và N là trung điểm của AC, mà AB = AC (2 cạnh bên của tam giác cân) ⇒ MB = NC
xét tam giác MBC và tam giác NCB, ta có :
MB = NC (cmt)
góc B = góc C (2 góc đáy của 1 tam giác cân)
BC là cạnh chung
⇒ tam giác MBC = tam giác NCB (c-g-c)
⇒ MC = NB (2 cạnh tương ứng)
c) xét tam giác NAG và tam giác NCK , ta có :
NA = NC (vì N là trung điểm của cạnh AC)
góc NAG = góc NCK (đối đỉnh)
NG = NK (gt)
=> tam giác NAG = tam giác NCK (c-g-c)
=> AG = CK (2 cạnh tương ứng)

B C A D E M N I H K
a) Ta thấy \(\widehat{ECN}=\widehat{ACB}\) (Hai góc đối đỉnh)
Tam giác ABC cân tại A nên \(\widehat{ACB}=\widehat{ABC}\Rightarrow\widehat{ECN}=\widehat{DBM}\)
Xét tam giác vuông BDM và CEN có:
BD = CE
\(\widehat{ECN}=\widehat{DBM}\) (cmt)
\(\Rightarrow\Delta BDM=\Delta CEN\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow BM=CN\) (Hai cạnh tương ứng)
b) Do \(\Delta BDM=\Delta CEN\Rightarrow MD=NE\)
Ta thấy MD và NE cùng vuông góc BC nên MD // NE
Suy ra \(\widehat{DMI}=\widehat{ENI}\) (Hai góc so le trong)
Xét tam giác vuông MDI và NEI có:
MD = NE
\(\widehat{DMI}=\widehat{ENI}\)
\(\Rightarrow\Delta MDI=\Delta NEI\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow MI=NI\)
Xét tam giác KMN có KI là đường cao đồng thời trung tuyến nên KMN là tam giác cân tại K.
c) Ta có ngay \(\Delta ABK=\Delta ACK\left(c-g-c\right)\Rightarrow\widehat{ABK}=\widehat{ACK}\) (1) và BK = CK
Xét tam giác BMK và CNK có:
BM = CN (cma)
MK = NK (cmb)
BK = CK (cmt)
\(\Rightarrow\Delta BMK=\Delta CNK\left(c-g-c\right)\Rightarrow\widehat{MBK}=\widehat{NCK}\) (2)
Từ (1) và (2) suy ra \(\widehat{ACK}=\widehat{NCK}\)
Chúng lại là hai góc kề bù nên \(\widehat{ACK}=\widehat{NCK}=90^o\)
Vậy \(KC\perp AN\)

a) Chứng minh ΔAIB = ΔCIK (c - g - c)
=> Góc BAC = Góc ACK
Chứng minh ΔAIK = ΔCIB (c - g - c)
=> Góc CAK = Góc ACB
Xét tam giác ABC và tam giác ACK có:
Góc BAC = Góc ACK (cmt)
AC: chung
Góc CAK = Góc ACB (cmt)
=> Tam giác ABC = Tam giác CKA (c - g - c)
=> AC = CK (2 cạnh tương ứng)
b) Tam giác ABC có AH là đường trung tueyesn, BI là đường trung tueeys, AH và BI cắt nhau tại G
=> G là trọng tâm của tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}AG=\dfrac{2}{3}AH\\CG=\dfrac{2}{3}CM\end{matrix}\right.\)
Có; \(AG+GH=AH\)
\(\Rightarrow\dfrac{2}{3}AH+GH=AH\)
\(\Rightarrow GH=\dfrac{1}{3}AH\)
\(\dfrac{AG}{GH}=\dfrac{\dfrac{2}{3}AH}{\dfrac{1}{3}AH}=2\)
Chứng minh tương tự: \(\dfrac{CG}{MG}=2\)
\(\Rightarrow\dfrac{AG}{GH}=\dfrac{CG}{MG}\left(=2\right)\)
=> MH // AC