Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

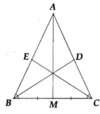
a) Chứng minh được ∆ A M B = ∆ A M C (c.c.c).
Từ đó suy ra AM là tia phân giác của góc BAC.
b) Xét tam giác ABC có AM, BD,CE là các tia phân giác. Từ tính chất ba đường phân giác trong tam giác, suy ra ba đường thẳng AM,BD,CE đồng quy.

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
b: \(BD=\sqrt{10^2-6^2}=8\left(cm\right)\)
d: Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)
nên ΔHBC cân tại H
=>HB=HC
hay H nằm trên đường trung trực của BC(1)
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,H,M thẳng hàng

Sorry, bạn tự vẽ hình nha!
a.
Tam giác ABC cân tại A có:
\(B=C=\frac{180-A}{2}=\frac{180-80}{2}=\frac{100}{2}=50\)
b.
Xét tam giác ABD và tam giác ACE có:
AB = AC (tam giác ABC cân tại A)
B = C (tam giác ABC cân tại A)
BD = CE (gt)
=> Tam giác ABD = Tam giác ACE (c.g.c)
=> AD = AE (2 cạnh tương ứng)
=> Tam giác ADE cân tại A
c.
Xét tam giác HAD vuông tại H và tam giác KAE vuông tại K có:
AD = AE (tam giác ADE cân tại A)
A1 = A2 (tam giác ABD = tam giác ACE)
=> Tam giác HAD = Tam giác KAE (cạnh huyền - góc nhọn)
=> AH = AK (2 cạnh tương ứng)

a) Xét △ABM vuông tại A và △DBM vuông tại D có:
BM chung
AB=DB=3cm(gt)
=> △ABM=△DBM (cạnh huyền-cạnh góc vuông) => AM=DM(2 cạnh t/ứ)
b) Xét △AMN và △DMC có:
AMN=DMC(2 góc đối đỉnh)
AM=DM(cmt)
MAN=MDC(gt)
=> △AMN=△DMC(g.c.g) => MN=MC(2 cạnh tướng ứng) => △MCN cân tại M
c) Vì △AMN=△DMC(cmt) => AN=DC(2 cạnh tương ứng)
Ta có AB=BD;AN=DC;BN=AN+AB;BC=BD+DC => BN=BC=> △BNC cân tại B
Vì △ABM=△DBM(cmt)=> ABM=DBM=> NBK=CBK (A thuộc BN; D thuộc BC;M thuộc BK) => BK là phân giác NBC
=> Trong △BNC cân tại B, BK là đường phân giác, đường trung trực, đường trung tuyến, đường cao,... (t/c) => BK là đường trung trực của CN
d) Áp dụng định lý Pytago vào △ABC vuông tại A có: AB2+AC2=BC^2
=> 9+16=25=BC^2 (cm) => BC = 5 cm
Ta có BD+DC=BC;BD=3cm=> DC=2cm
Ta có AN=DC(cmt) => AN=2cm
Áp dụng định lý Pytago vào △ANC vuông tại A có:
AN^2+AC^2=NC^2
=> 4+16=NC^2
=> NC= căn 20 = 2 x căn 5 (cm)
Vì BK là trung trực NC => K là trung điểm NC => KC = 1/2 NC = căn 5 (cm)
Áp dụng định lý Pytago vào △BKC vuông tại K có:
BC^2=BK^2+KC^2 => BK^2=BC^2+KC^2=25-5=20cm => BK=căn 20=2 nhânnhân căn 5 (cm)

BD, CE ở đâu vậy bạn?