Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AH , BK cac duong cao
ke HF vuong goc AC=>HF//=BE/2=6
( tgBCE co HF duong trung binh)
tgiac AHC vuong tai H , duong cao HF
ta co 1/HF^2=1/AH^2+1/HC^2
=>HC=HF*AH/can(AH^2-HE^2)=6.5
=>BC=2HC=13
2)ta co b^2=a.b' ; c^2=a.c' vay b'/c'=(b/c)^2
do đó BD/CD=AB/AC(tinh chat duong pgiac)
vay BH/CH=(BD/CD)^2=BD^2/CD^2
ap dung tinh chat ty le thuc
BH/(CH+BH)=BD^2/(BD^2+CD^2)
BH/BC=BD^2/(BD^2+CD^2)
vi BH+CH=BC=>thay so vao BH=6.3
vay HD=BD-BH=1.2
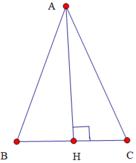
Kẻ AH vuông góc với BC, BK vuông góc với AC.
Tam giác ABC cân tại A nên AB = AC.
SABC = ½ AH . BC = ½ AH . 2BH (vì AH là đường cao của tam giác ABC cân tại A nên AH cũng là đường trung tuyến.→ BH = CH)
SABC = ½ BK. AC
Do đó: ½ AH. 2BH = ½ BK. AC
→ AH . BH = ½ BK . AC
→ 15,6 . BH = ½ . 12. AB (AB = AC)
→ 15,6 . BH = 6. (AH + BH)
→ 15,6 / 6 .BH = 15,6 + BH
→ 2,6 BH = 15,6 + BH
→ 2,6 BH – BH = 15,6
→ 1,6 BH= 15,6
→ BH = 15,6 : 1,6
→ BH = 9,75
→ BC = 2. 9, 75 = 19,5

Làm trên này là fai có cáh giải nuk cháu ak, ghi kq chỉ tổ tốn côg

BẠn chỉ mình vẽ bán kính trên hoc24.vn đi rồi mình giải cho

a/Áp dụng định lí Pytago và tam giác ABC vuông tại A:
BC2=AB2+AC2
=>AC2=BC2-AB2=102-62=100-36=64
=> AC=\(\sqrt{64}=8cm\)
b/ Xét tam giác ABC và tam giác ADC có:
AC chung
góc BAC=DAC=90 độ
AD=AB(gt)
=> Tam giác ABC=tam giác ADC(c-g-c)

Đáp án B
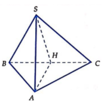
Gọi H là trung điểm B C ⇒ A H ⊥ B C → S B C ⊥ A B C A H ⊥ S H .
Xét hai tam giác vuông SHA và BHA có H A chung S A = B A = a ⇒ Δ S H A = Δ B H A .
⇒ S H = B H = C H ⇒ Δ S B C vuông tại S ⇒ R b = B H = B C 2 .
Dễ thấy
G T = B C ⇒ R = R b 2 + R d 2 − G T 2 4 = B H 2 + R d 2 − B C 2 4 = R d = a
Xét tam giác ABC, có:
sin C = A B 2 R = 1 2 ⇒ cos C = 3 2 ⇒ B C = 2 H C = 2 A C . cos C = a 3
Trong tam giác vuông SBC, ta có S C = B C 2 − S B 2 = a 2 .

Đáp án C
Gọi H là trung điểm B C ⇒ A H ⊥ B C ⇒ A H ⊥ S H
Ta có Δ S H A = Δ B H A , Δ S B C vuông tại S ⇒ R b = B H = B C 2
R = R b 2 + R d 2 − B C 2 4 = a
Xét Δ A B C có
sin C = A B 2 R = 1 2 ⇒ cos C = 3 2 ⇒ B C = 2 H C = a 3
Ta có trong tam giác vuông S B C : S C = B C 2 − S B 2 = a 2

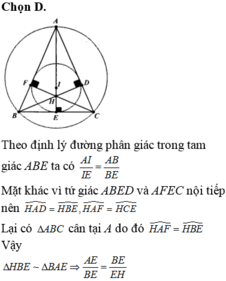

BC và AK cắt BC tại H.Ta có HB=HC (AK là trung trực của BC)
=>HC=BC/2.
AH=√(AC²-CH²);
∆ACH~∆COH (tam giác vuông chung góc nhọn tại O)
=>AH/AC=HC/CO=>CO=AC.HC/AH.
=20.12/√(20²-12²)=20.12/16=15.
Gọi AH, BK là hai đường cao, có AH = 10; BK = 12
thấy hai tgiác CAH và CBK đồng dạng => CA/AH = CB/BK
=> CA/10= 2CH/12 => CA = 2,6.CH (1)
mặt khác áp dụng pitago cho tgiac vuông HAC:
CA² = CH² + AH² (2)
thay (1) vào (2): 2,6².CH² = CH² + 102
=> (2,6² - 1)CH² = 102=> CH = 10 /2,4 = 6,5
=> BC = 2CH = 13 cm