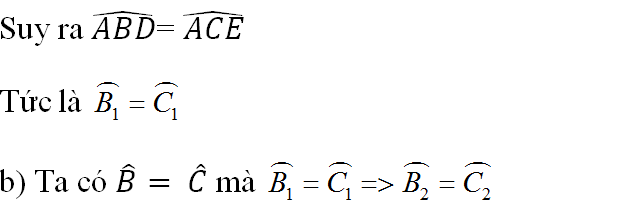Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

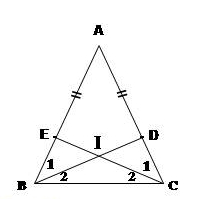
∆ABD và ∆ACE có:
AB=AC(gt)
ˆA góc chung.
AD=AE(gt)
Nên ∆ABD=∆ACE(c.g.c)
Suy ra: ˆABD=ˆACE.
Tức là ˆB1 =ˆC1
b) Ta có ˆB=ˆC mà ˆB1=ˆC1 suy ra ˆB2=ˆC2
Vậy ∆IBC cân tại I

tớ chỉ làm đc ý a, k biết bạn có cần k
bạn tự vẽ hình nhé :)
a, xét tam giác ADB và tam giác AEC ta có:
góc ABC= góc ACB(tam giác ABC cân)
BD=EC( gt)
AB=AC (tam giác ABC cân)
=>tam giác ADB= tam giác AEC (c-g-c)

A E B M D C 1 1 2 2 1 2
a, Ta có \(\Delta ABC\)cân tại A
=>AB=AC
+)Xét \(\Delta ABD\)và \(\Delta ACE\) có
AB=AC (cmt)
\(\widehat{BAC}\): chung
AD=AE (gt)
=> \(\Delta ABD\)= \(\Delta ACE\) (c-g-c)
=> \(\widehat{ABD}=\widehat{ACE}\) ( 2 góc t/ứ)
b, Ta có \(\hept{\begin{cases}\widehat{ABC}=\widehat{ACB}\\\widehat{ABD}=\widehat{ACE}\left(cmt\right)\end{cases}}\)(t/c t/g cân)
=> \(\widehat{B_2}=\widehat{C_2}\)
Xét \(\Delta IBC\)có \(\widehat{B_2}=\widehat{C_2}\)=> \(\Delta IBC\)cân tại I
Xin lỗi nhé mình chưa nghĩ ra câu b và câu c