Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

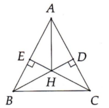
a, Xét ∆ ABD và ∆ ACE có:
Góc D = góc E = 90°
AB = AC (∆ ABC cân)
Góc BAC chung
➡️∆ ABD = ∆ ACE (ch-gn)
➡️AD = AE (2 cạnh t/ư)
b, ✳️C/m AH là tia phân giác của góc BAC
Xét∆ ABC cân tại A có:
BD vuông góc với AC
CE vuông góc với AB
H là giao điểm của BD và CE
➡️H là trực tâm ∆ ABC
➡️AH vuông góc với BC
mà ∆ ABC cân tại A
➡️AH là đg cao đồng thời là đg phân giác
➡️AH là p/g góc BAC(đpcm)
✳️C/m AH là đg trung trực của ED
Xét ∆ AED cân tại A (AD = AE)
➡️AH là đg phân giác đồng thời là đg trung trực
➡️AH là đg trung trực của ED (đpcm)
c, Xét ∆ AEH và ∆ ADH có:
AE = AD (cmt)
Góc BAH = góc CAH (cmt)
AH chung
➡️∆ AEH = ∆ ADH (c.g.c)
➡️HE = HD (2 cạnh t/ư)
Xét ∆ CDH vuông tại D
➡️CH > HD
mà HE = HD (cmt)
➡️CH > HE
Còn câu d để mk nghĩ đã nhé
Câu d nè bn.
d, Vì AH là đg trung trực của EF và AH vuông góc với BC
➡️ED // BC (quan hệ từ vuông góc đến song song)
Ta có: góc FED = góc DBC (2 góc có 2 cạnh tương ứng song song)
Gọi AH giao BC tại M
Xét ∆ ABC cân tại A
➡️AH là đg cao đồng thời là trung tuyến
HM là trung tuyến của BC
Xét ∆ IBC có HM là đg cao đồng thời là trung tuyến
➡️∆ IBC cân tại I
➡️Góc DBC = góc ECB
Mà góc ECB = góc DEC (2 góc so le trong)
➡️Góc DEC = góc DBC
mà góc DBC = góc FED (cmt)
➡️Góc FED = góc DEC
➡️ED là tia phân giác góc FEC
Xét ∆ FEC có: CI là phân giác góc DCE (gt)
EI là phân giác góc FEC (cmt)
CI và EI giao nhau tại I
➡️I là tâm đg tròn nội tiếp∆ FEC
➡️FI là phân giác góc CFE
mà góc CFE vuông (EF // BD, góc BDC = 90°)
➡️Góc EFI = góc CFI = 90° ÷ 2 = 45°
Vậy góc EFI = 45°
Hok tốt nhé~

a/ Xét \(\Delta ABD\left(D=1v\right)\) và \(\Delta ACE\left(E=1v\right)\) có:
góc A chung (gt)
AB = AC (\(\Delta ABC\) cân tại A)
=> \(\Delta ABD=\Delta ACE\) (ch-gn)
b/ Xét\(\Delta ABK\left(K=1v\right)\) và \(\Delta ACK\left(K=1v\right)\) có:
AB = AC (\(\Delta ABC\) cân tại A)
AK chung (gt)
=> \(\Delta ABK=\Delta ACK\) (ch-cgv)
=> góc BAK = góc CAK (hai góc tương ứng)
=> AK là tia phân giác của góc BAC

Chú ý H là trực tâm tam giác ABC, từ đó AH vừa là đường cao vừa là đường phân giác

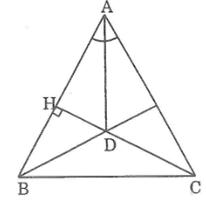
BÀI 1 cho tam giác ABC vuông tại A.Kẻ BD là phân giác của góc B.Kẻ AI vuông góc BD tại I.AI cắt BC tại E
a) chứng minh AB=EB
b) chứng minh tam giác BED vuông
c) DE cắt AB tại F, chứng minh AE//FC
BÀI 2 cho tam giác ABC cân tại A, có BD và CE là hai đường trung tuyến cắt nhau tại I
a) chứng minh tam giác IBC cân
b)lấy O thuộc tia IC sao cho IO=IE.Gọi K là trung điểm của IA.Chứng minh AO, BD, CK đồng quy
BÀI 3 cho tam giác ABC cân tại A, kẻ tia phân giác của góc BAC cắt BC tại H.Biết AB=15cm, BC=18cm
a)so sánh góc A và góc C
b)chứng minh rằng tam giác ABH = tam giác ACH
c)vẽ trung tuyến BD của tam giác ABC cắt AH tại G.Chứng minh rằng: tam giác AEG = tam giác ADG
d)tính độ dài AG
e) kẻ đường thẳng CG cắt AB ở E, chứng minh rằng: tam giác AEG = tam giác ADG
BÀI 4 cho tam giác ABC vuông tại A, trên BC lấy điểm D sao cho BA=BD.Qua D kẻ đường vuông góc với BC cắt AC tại E, qua C kẻ đường vuông góc với BE tại H cắt AB tại F
a)chứng minh tam giác ABE = tam giác DBE
b) chứng minh tam giác BCF cân
c) chứng minh 3 điểm F.D,E thẳng hàng
d)trên cạnh CB lấy điểm M sao cho CA=CM.Tính số đo góc DAM
BÀI 5 cho tam giác ABC cân tại A, kẻ BD vuông góc AC, kẻ CE vuông góc AB, BD và CE cắt nhau tại I
a)chứng minh rằng tam giác BDC = tam giác CEB
b)so sánh góc IBE và góc ICD
c) đường thẳng AI cắt BC tại H, chứng minh AI vuông góc BC tại H
BÀI 6 cho tam giác ABC vuông tại A, biết AB=6cm, AC=8cm
a)tính BC
b)trung trực của BC cắt AC tại D và cắt AB tại F, chứng minh góc DBC=DCB
c) trên tia đối của tia DB lấy E sao cho DE=DC, chứng minh tam giác BCE vuông và DF là phân giác góc ADE
d) chứng minh BE vuông góc FC
Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).

a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
CB chung
góc EBC=góc DCB
=>ΔEBC=ΔDCB
b: Xét ΔHBC có góc HCB=góc HBC
nên ΔHBC cân tại H
c: Xet ΔABH và ΔACH có
AB=AC
BH=CH
AH chung
=>ΔABH=ΔACH
=>góc BAH=góc CAH
=>AH làphân giác của góc BAC

b) Xét tam giác ABC có:
BD là đường cao của ABC (gt)
CE là đường cao của ABC (gt)
mà BD cắt CE tại H (gt)
=>AH là đường cao thứ 3
=>AH vuông góc BC
c) Ta có: Tam giác ABC cân tại A (gt)
=> góc ABC = góc ACB = 70o
Xét tam giác ABC CÓ
ABC + ACB + BAC =180 (tổng 3 góc trong tam giác)
70 + 70 + BAC = 180
BAC = 180 - 140 = 40o
Ta có: Tam giác ABC cân tại A, đường cao AH (gt)
=>AH là đường phân giác của BAC
=>BAH = CAH = BAC : 2 =40 : 2= 200
Xét tam giác EAH và tam giác DAH có;
EAH = DAH =200
AH chung
=>EAH = DAH(ch_gn)
=> AHE = AHD=90-20=60o( 2 góc tương ứng)
Ta có: EHD = AHE + AHD = 60 + 60 =1200
=> BHC = EHD =1200 ( 2 góc đối đỉnh)

Theo mình nghĩ bài này nhầm đầu bài rồi... Tam giác ABC cân tại A mà góc A bằng 90 độ=> Tam giác ABC là tam giác vuông cân.... Xong đó ta lại kẻ tiếp BD vuông góc với AC Thì BD sẽ Trùng với BA, Tiếp nữa kẻ CE vuông góc vớiAB thì đoạn CE sẽ trùng với đoạn AC
Theo mình nghĩ đầu bài nên để tam giác ABC là tam giác cân thì hợp hơn... Góc A không bằng 90 độ
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).
Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ - 70^\circ - 70^\circ = 40^\circ \).
b) Xét tam giác vuông ADB và tam giác vuông AEC có:
AB = AC (tam giác ABC cân);
\(\widehat A\) chung.
Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).
c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.
Xét hai tam giác vuông AFB và AFC có:
AB = AC (tam giác ABC cân);
AF chung.
Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).
Vậy tia AH là tia phân giác của góc BAC.