Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
góc KBC=goc HCB
=>ΔKBC=ΔHCB
=>BK=HC
=>AK=AH
b: Xét ΔABC có AK/AB=AH/AC
nên KH//BC

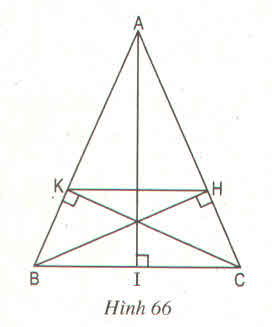
a) Xét 2 tam giác vuông: \(\Delta KBC\) và \(\Delta HCB\)
\(\widehat{KBC}=\widehat{HCB}\)
\(BC\) chung
suy ra: \(\Delta KBC=\Delta HCB\)(ch_gn)
\(\Rightarrow\)\(BK=CH\)
b) \(AB=AC\) VÀ \(BK=CH\)
\(\Rightarrow\)\(\frac{BK}{AB}=\frac{HC}{AC}\)
\(\Rightarrow\) \(KH//BC\) (theo định lý Ta-lét đảo)

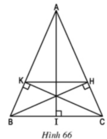
A B C H K I
a, tg ABC cân tại A (gt) => ^ABC = ^ACB (tc)
xét tg HCB và tg KBC có : BC chung
^CHB = ^BKC = 90
=> tg ABC = tg KBC (ch-gn)
=> CH = BK (đn)
=> CH/AB = BK/AB mà AB = AC do tam giác ABC cân tại A (Gt)
=> CH/AC = BK/AB
=> HK // BC (đl)
b, sửa đề thành HC.AC = BC.IC
xét tg CHB và tg CIA có : ^ACB chung
^CHB = ^AIC = 90
=> tg CHB đồng dạng với tg AIC (g-g)
=> HC/BC = IC/AC (đn) => HC.AC = BC.IC
c, tg ABC cân tại A (Gt) mà AI là đường cao (gt)
=> AI đồng thời là đtt (đl) => IB = IC = 1/2 BC
mà có : HC.AC = BC.IC (Câu b) ; BC = a; AC = b
=> HC.b = a.a/2 => BC = a^2/2b
Có AH = AC - HC
=> AH = b - a^2/2b = (2b^2 - a^2)/2b
mà HK // BC (câu a) nên
AH/AC = HK/BC => HK = AH.BC/AC = a/b.(2b^2 - a^2)/2b
=> HK = (2ab^2 - a^3)/2b^2 = a - a^3/2b^2

A B C I K H
a, Xét tam giác BKC và CHB có :
BC chung
\(\widehat{ABC}=\widehat{ACB}\)( vì tam giác ABC cân tại A )
\(\widehat{BKH}=\widehat{BHC}=90^o\)
\(\Rightarrow\Delta BKC=\Delta CBH\left(ch-gn\right)\)
\(\Rightarrow BK=CH\)( 2 cạnh tương ứng )
b, bạn thông cảm mình chưa nghĩ ra ^^
c, Ta có : AB = AC ( tam giác ABC cân tại A )
\(BK=CH\left(\Delta BKC=\Delta CHB\right)\Rightarrow AK=AH\)
Do đó : \(\frac{AK}{AB}=\frac{AH}{AC}\Rightarrow KH//BC\)( định lí Talet đảo )
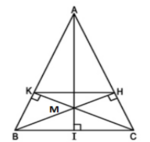
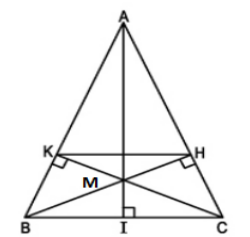
d, BK cắt CK tại M
=> M là trực tâm của tam giác ABC
=> \(AM\perp AC\)tại I
Ta có : \(\Delta AIC~BHC\)vì \(\widehat{I}=\widehat{H}=90^o\)và C chung
\(\Rightarrow\frac{IC}{HC}=\frac{AC}{BC} hay \frac{\frac{a}{2}}{HC}=\frac{b}{a}\Rightarrow HC=\frac{a^2}{2b}\)
\(\Rightarrow AH=b-\frac{a^2}{2b}=\frac{2b^2-a^2}{2b}\)
Mà HK//BC =>\(\frac{HK}{BC}=\frac{AH}{AC}\Rightarrow HK=\frac{BC.AH}{AC}\)
\(\Rightarrow HK=\frac{a}{b}\left(\frac{2b^2-a^2}{2b}\right)=\frac{2ab^2-a^3}{2b^2}=a-\frac{a^3}{2b^2}\)