Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Con tham khảo tại link dưới đây nhé:
Câu hỏi của Dương Ánh Ngọc - Toán lớp 8 - Học toán với OnlineMath

:a,nối E với D,ED là đường trung bình nên ED=4cm
MN là đường trung bình hình thang BEDC nên MN=(8+4):2=6
b,vì MI // ED và M là trung điểm BE => MI là đường trung bình ∆BED
MI=1/2 ED,tương tự ta có KN=MI=1/2 ED (*)
vì ED=1/2 BC mà ∆EDG∞∆IKG∞CBG(G là giao 2 tiếp tuyến)
nên IK=1/2 ED <=> kết hợp với(*)ta có KN=MI=IK=1/2ED
Bài2:gọi đoạn nối trung điểm 2 cạnh AB và AC của tứ giác ABCD là MN,ta có MN=1/2 BC,trong ∆BCD có BC<BD+CD nên MN< BD+CD(bất đẳng thức tam giác)
Bai3:gọi tứ giác đó là ABCD,MN là cạnh nối trung điểm,kéo dài AN giao DC tại E,ta có AB=CE ,nên ta có ∆ABN=∆CEN =>gocBAN=góc CEN.Mà 2 góc nằm ở vị trí so le trong nên AB // DC => ABCD là hình thang.
Bai4:a,kẻ BK // AD,ta có hình bình hành ABKD =>IE là hiệu 2 đáy,kẻ đường cao BH',ta có ∆BCH'=∆ADH,mà ∆BIE cân nên H' là trung điểm IE =>HD=1/2(DE-AB)
b,kẻ BG // với AC,ta có hình bình hành ABGC =>AB=CG
vì ABH'H là hình vuông=>AB=HH'=>HH'=CG mà H'C=DH nên ta có
HH'+H'C=CG+DH mà (HH'+H'C)+(CG+DH)=DG=DC+AB
=>HH'+H'C=HC=1/2(DC+AB)
Bài5:Từ M kẻ MM' vuông góc với d,ta có MM'//BB'//CC'
mà M là trung điểm BC nên MM' là đường trung bình hình thang BB'C'C,ta lại có O là trung điểm AM=>∆AA'O=∆MM'O nên AA'=MM'
ta có MM'=AA'=(BB'+CC'):2
Bài6:Kẻ MN//AB//DC =>MN=(7+3)/2=5 =>∆ANM và∆DNM cân tại N
góc AMN=(180độ-gócANM)/2
góc DMN=(180độ-gócDNM)/2
góc AMN+góc DMN=(180độ-gócANM+180độ-gócDNM)/2
=(360độ-180độ)/2=90độ=gócAMD=>AM vuông góc với DM
còn 3 bài cuối bác nào khỏe tay thì giúp cháu nó hộ em với,em mỏi tayquá rồi
Chi tiết thêm:
lâu lắm mới vào lại câu này
Bài7:từ C kẻ đường vuông góc với BE tại M
kéo dài CM giao AB tại N
Ta có ∆CME đồng dạng với ∆CAN (gg)
=>góc CEM= góc CNA
vì góc CEM= góc AEB (đối đỉnh)
=> góc CNA= góc AEB
=>∆CAN=∆BAE(góc nhọn,cạnh góc vuông,góc 90º)
=>AE=AN=AD
vì AN=AD
mà AK // CN
=> AK là đường trung bình hình thang CIDN
=>IK=KC

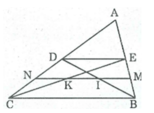
Trong ∆ ABC ta có: E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
⇒ ED // BC và ED = 1/2 BC
(tính chất đường trung bình của tam giác)
+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung hình hình thang BCDE ⇒ MN // DE
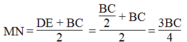
(tính chất đường trung bình hình thang)
Trong ∆ BED, ta có: M là trung điểm BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
⇒ MI = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
Trong ∆ CED ta có: N là trung điểm CD
NK // DE
Suy ra: NK là đường trung bình của ∆ CED
⇒ NK = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
IK = MN – (MI + NK) = 3/4 BC – (1/4 BC + 1/4 BC) = 1/4 BC
⇒ MI = IK = KN = 1/4 BC

A C B E D I K M N
Hình trên, đặt BC = a
Vì \(\Delta ABC\)có \(AE=EB;AD=DC\)nên \(ED\)là đường trung bình . Do đó ED song song BC và \(ED=\frac{BC}{2}=\frac{a}{2}\)
Do MN là đường trung bình của hình thang BEDC nên MN song song ED song song BC
\(\Delta BED\)có \(BM=ME;MI\)song song \(ED\)nên \(MI\)là đường trung bình , \(MI=\frac{ED}{2}=\frac{a}{4}\)
\(\Delta CED\)có \(CN=ND;NK\)song song \(ED\)nên \(NK\)là đường trung bình ,\(NK=\frac{ED}{2}=\frac{a}{4}\)
\(\Delta EBC\)có \(EM=MB;MK\)song song \(BC\)nên \(MK\)là đường trung bình ,\(MK=\frac{BC}{2}=\frac{a}{2}\)
\(\Rightarrow IK=MK-MI=\frac{a}{2}-\frac{a}{4}=\frac{a}{4}\)
Vậy \(MI=IK=KN\)

a:
Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: ED//BC
Xét hình thang BEDC có
M là trung điểm của EB
N là trung điểm của DC
Do đó: MN là đường trung bình của hình thang BEDC
Suy ra: MN//ED//BC
Xét ΔEBD có
M là trung điểm của EB
MI//ED
Do đó: I là trung điểm của BD
Xét ΔEDC có
N là trung điểm của DC
NK//ED
Do đó: K là trung điểm của EC
Xét ΔEBC có
M là trung điểm của EB
K là trung điểm của EC
Do đó: MK là đường trung bình của ΔEBC
Suy ra: \(MK=\dfrac{BC}{2}\left(1\right)\) và MK//BC
Xét ΔDBC có
I là trung điểm của BD
N là trung điểm của DC
Do đó: IN là đường trung bình của ΔDBC
Suy ra: \(IN=\dfrac{BC}{2}\left(2\right)\)
Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: \(ED=\dfrac{BC}{2}\left(3\right)\)
Từ (1), (2) và (3) suy ra MK=IN=ED

A B C E D M N I K
Xét tg ABC có: E là t/đ của AB (gt) và D là t/đ của AC (gt)
=> DE là đg trung bình của tg ABC => ED = 1/2. BC ; ED//BC
Xét hthang EDCB(ED//BC) có: M là t/đ của BE (gt) và N là t/đ của DC(gt)
=> MN là đg trung bình của hthang EDCB => MN//DE//BC ; MN = 1/2.(DE+BC) . MÀ DE=1/2.BC (cmt)=> MN=3/2 . DE
=> MI+IK+KN =3/2 . DE (1)
xét tg BDE có: M là t/đ của BE(gt) ; MI//ED ( vì I thuộc MN ; MN//DE) => I là r/đ của BD => MI là đg trung bình của tg BDE
=> MI =1/2.DE (2)
C/m tương tự ta đc: KN là đg trung bình của tg CDE => KN= 1/2.DE (3)
Từ (2) ,(3)=> MI=KN =1/2.DE (*)
Thay (2),(3) vào (1) ta đc: 1/2. DE +IK +1/2. DE =3/2. DE => IK =1/2. DE (**)
Từ (*),(**)=> MI=IK=KN (đpcm)
Bạn có thể giải thích cho mình vì sao = 1/2.(DE+BC)Mà DE = 1/2BC => MN =3/2 là sao vậy mình không hiểu đoạn đó
Do BD là đường trung tuyến của ∆ABC (gt)
⇒ D là trung điểm của AC
Do CE là đường trung tuyến của ∆ABC (gt)
⇒ E là trung điểm của AB
⇒ DE là đường trung bình của ∆ABC
⇒ DE // BC và DE = BC : 2
⇒ BC = 2DE
Do DE // BC (cmt)
⇒ BCDE là hình thang
Do M là trung điểm của BE (gt)
N là trung điểm của CD (gt)
⇒ MN là đường trung bình của hình thang BCDE
⇒ MN // DE // BC và MN = (DE + BC) : 2
Do MN // DE (cmt)
⇒ MI // DE và NK // DE
∆BDE có:
MI // DE (cmt)
M là trung điểm của BE (gt)
⇒ I là trung điểm của BD
⇒ MI là đường trung bình của ∆BDE
⇒ MI = DE : 2 (1)
∆CDE có:
NK // DE (cmt)
N là trung điểm của CD (gt)
⇒ K là trung điểm của CE
⇒ NK là đường trung bình của ∆CDE
⇒ NK = DE : 2 (2)
Mà MI = DE : 2
⇒ MI = NK = DE : 2
⇒ MI + NK = DE
Ta có:
MN = (DE + BC) : 2
Mà BC = 2DE (cmt)
⇒ MN = (DE + 2DE) : 2
= DE + DE : 2
Lại có:
MN = MI + IK + NK
= (MI + NK) + IK
= DE + IK
⇒ DE + IK = DE + DE : 2
⇒ IK = DE : 2 (3)
Từ (1), (2) và (3) ⇒ MI = IK = KN
Xét Δ���ΔBED có {��//����=��{MI//EDME=BM suy ra ��=��ID=IB.
Xét Δ���ΔCED có {��//����=��{NK//EDNC=ND suy ra ��=��KE=KC.
Suy ra ��=12��MI=21ED; ��=12��NK=21ED; ��=12��ED=21BC.
��=��−��=12��−12��=��−12��=12��IK=MK−MI=21BC−21DE=DE−21DE=21DE.
Vậy ��=��=��MI=IK=KN.