
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tam giác ABC vuông tại A, B=60.
⇒ Tam giác ABC là 1 nửa tam giác đều
⇒AB = \(\frac{BC}{2}\) =4cm.
AC=12‐4=8cm
Vậy AB=4cm
AC=8cm
A B C 2x 60* H
Kẻ: \(AH\perp BC\).Đặt \(AB=2x\Rightarrow BH=x\Rightarrow AH=x\sqrt{3};HC=8-x\)
Áp dụng định lí Pi-ta-go có:
\(AC=\sqrt{\left(x\sqrt{3}\right)^2+\left(8-x\right)^2}=\sqrt{4x^2-16x+64}\)
Do \(AB+AC=12\Rightarrow2x+\sqrt{4x^2-16x+64}=12\)
Giải phương trình có x = 2,5
\(\Rightarrow AB=2x=2.2,5=5cm\)
Thay số vào tính được AC =))

A B C H
Từ B dựng đường thẳng vuông góc với AC cắt AC tại H
Xét tg vuông ABH có
\(\widehat{ABH}=90^o-\widehat{A}=90^o-60^o=30^o\)
\(\Rightarrow AH=\dfrac{AB}{2}=\dfrac{3}{2}=1,5cm\) (trong tg vuông cạnh đối diện góc 30 độ bằng nửa cạnh huyền)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-1,5^2}\)
Xét tg vuông BCH
\(\widehat{ACB}=30^o\)
=> \(BH=\dfrac{BC}{2}\Rightarrow BC=2.BH\) (lý do như trên)
Bạn tự thay số và tính nốt nhé
Xin lỗi mình nhầm từ chô \(\widehat{ACB}=30^o\)
Ta có
\(CH=AC-AH\)
Xét tg vuông BCH
\(BC=\sqrt{BH^2+CH^2}\)



a. tám giác ABC có A=90, B=60 => C=30
trong 1 tam giác vuông, cạnh đối diện với góc 30 độ thì =1/2 cạnh huyền
=> 2AB=BC hay BC=12
áp dụng đlý pytago vào ABC, ta tính đc AC=\(6\sqrt{3}\)
b. tam giác ABC có BD là tia phân giác góc B =>\(\frac{AD}{DC}=\frac{AB}{BC}< =>\frac{AD}{AB}=\frac{DC}{BC}=>\frac{AD+DC}{AB+BC}=\frac{AC}{6+12}=\frac{6\sqrt{3}}{18}\)
=>\(\frac{AD}{AB}=\frac{6\sqrt{3}}{18}=>AD=\frac{6\sqrt{3}.6}{18}=2\sqrt{3}\)
áp dụng đlý pytago vào ABD => BD=\(4\sqrt{3}\)


bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ
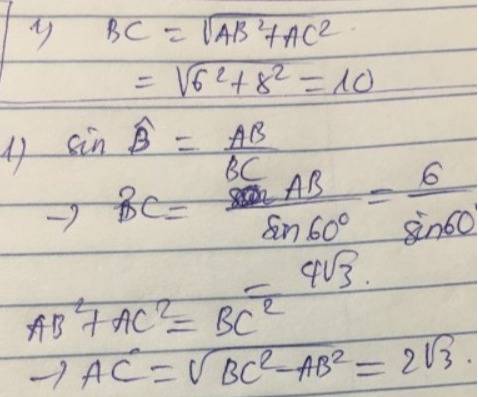
Theo bất đẳng thức tam giác, ta có:
\(AB+BC>AC< AB-BC\)
\(\Rightarrow6+4>AC< 6-4\)
\(\Rightarrow10>AC< 2\)
.....
Còn dữ liệu B = 60 độ em ko bt lm sao để giải AC chính xác, dù j e cx chỉ ms lớp 7 nên lm đc cách này thôi
nhầm, đổi dấu < thành > nhé