Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\frac{{AB}}{{DE}} = 2{;^{}}\frac{{BC}}{{EF}} = 2{;^{}}\frac{{AC}}{{DF}} = 2\)
Ta có:\(\dfrac{AB}{DE}=2;\dfrac{BC}{EF}=2;\dfrac{AC}{DF}=2\)

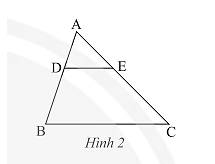
A E C B D a) Theo bài ra ta có:\(\frac{AE}{EC}=\frac{3}{4}\)=> \(\frac{AE}{EC+AE}=\frac{3}{4+3}\Rightarrow\frac{AE}{AC}=\frac{3}{7}\)
Xét ΔABC có DE//BC => \(\frac{DE}{BC}=\frac{AE}{AC}=\frac{3}{7}\) (hệ quả đ/lí Ta-lét)
=> DE = \(\frac{3}{7}BC=\frac{3}{7}.28=12\left(cm\right)\)
b) Xét ΔABC có DE//BC => \(\frac{AD}{BD}=\frac{AE}{EC}\) (đ/lí Ta-lét)
Mà \(\frac{AD}{BD}=\frac{EC}{AE}\left(gt\right)\) => \(\frac{AE}{EC}=\frac{EC}{AE}\) (=\(\frac{AD}{BD}\))
=>AE2=EC2 => AE = EC
=> E là trung điểm của AC.
Xét ΔABC có: DE//BC ; E là trung điểm của AC (cmt)
=> D là trung điểm của AB
Chúc bạn học tốt!

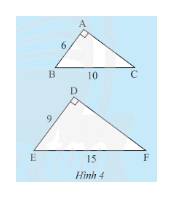
a) Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {6^2} + A{C^2} = {10^2} \Leftrightarrow A{C^2} = {10^2} - {6^2} = 64 \Leftrightarrow AC = 8\).
Xét tam giác \(DEF\) vuông tại \(D\) ta có:
\(D{E^2} + D{F^2} = E{F^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {9^2} + D{F^2} = {15^2} \Leftrightarrow D{F^2} = {15^2} - {9^2} = 144 \Leftrightarrow DF = 12\).
b) Tỉ số:
\(\frac{{AB}}{{DE}} = \frac{6}{9} = \frac{2}{3};\frac{{AC}}{{DF}} = \frac{8}{{12}} = \frac{2}{3}\); \(\frac{{BC}}{{EF}} = \frac{{10}}{{15}} = \frac{2}{3}\).
Do đó, \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\).
c) Xét tam giác\(ABC\) và tam giác\(DEF\) có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta DEF\) (c.c.c)

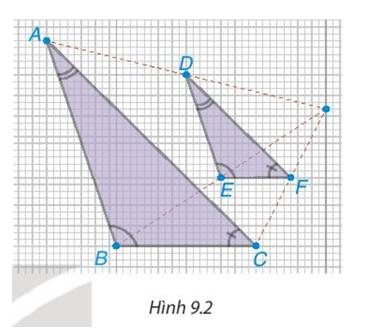
a) Vì \(\left\{ \begin{array}{l}JC \bot AE\\BH \bot AE\end{array} \right. \Rightarrow JC//BH\). Vì \(JC//BH \Rightarrow \widehat {HBA} = \widehat {JCA}\) (hai góc đồng vị)
hay \(\widehat {HBA} = \widehat {DCB}\)
Xét \(\Delta ABH\) và \(\Delta DCB\) có:
\(\widehat {HBA} = \widehat {DCB}\) (chứng minh trên)
\(\widehat {AHB} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta ABH\backsim\Delta DCB\) (g.g)
b) Vì (hai góc tương ứng) hay \(\widehat {EAB} = \widehat {CDB}\).
Xét \(\Delta AEB\) và \(\Delta DCB\) có:
\(\widehat {EAB} = \widehat {CDB}\) (chứng minh trên)
\(\widehat {ABE} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta AEB\backsim\Delta DCB\) (g.g)
Suy ra, \(\frac{{BE}}{{BC}} = \frac{{BA}}{{BD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Hay \(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\) (điều phải chứng minh).


Chọn D
Vì \(DE//BC\) nên theo định lí Thales và hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}};\frac{{BD}}{{AD}} = \frac{{EC}}{{AE}};\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}};\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).