Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

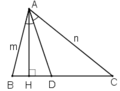
Kẻ AH là đường cao của tam giác ABC
Ta có:

Vậy tỉ số diện tích của tam giác ABD và tam giác ACD bằng m/n.

a/ Theo tính chất đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy ta có
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{m}{n}\)
Hai tam giác ABD và tam giác ACD có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{BD}{CD}=\frac{m}{n}\)
b/ Ta có
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{m}{n}\Rightarrow\frac{S_{\Delta ABD}}{m}=\frac{S_{\Delta ACD}}{n}=\frac{S_{\Delta ABD}+S_{\Delta ACD}}{m+n}=\frac{S_{\Delta ABC}}{m+n}=\frac{s}{m+n}\)
\(\Rightarrow S_{\Delta ABD}=\frac{sm}{m+n}\)
Xét hai tam giác ABM và tam giác ABC có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABM}}{S_{\Delta ABC}}=\frac{BD}{BC}=\frac{1}{2}\Rightarrow S_{\Delta ABM}=\frac{S_{\Delta ABC}}{2}=\frac{s}{2}\)
Mà \(S_{\Delta ADM}=S_{\Delta ABM}-S_{\Delta ABD}=\frac{s}{2}-\frac{sm}{m+n}\)

Kẻ AH ⊥ BC
Ta có:
SABD = 1212AH.BD
SADC = 1212AH.DC
=>SSBDSADCSSBDSADC = 12AH.BD12AH.DC12AH.BD12AH.DC = BDDCBDDC
Mặt khác: AD là đường phân giác của ∆ABC
=> BDDCBDDC= ABACABAC = mnmn.
Vậy SSBDSADCSSBDSADC = mn
kẻ AH là đường cao của tam giác ABD và cũng là đường cao của tam giác ACD.
\(\dfrac{SABD}{SACD}=\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.DC}=\dfrac{BD}{DC}\) (1)
TA CÓ:\(\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{m}{n}\left(2\right)\)
Từ (1) và (2) =>\(\dfrac{SABD}{SADC}=\dfrac{m}{n}\)

A B C D H E K I F
a) Xét t/giác HBA và t/giác ABC
có: \(\widehat{B}\):chung
\(\widehat{BHA}=\widehat{A}=90^0\)(gt)
=> t/giác HBA đồng dạng t/giác ABC (g.g)
b) Xét t/giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2 (định lí Pi - ta - go)
=> AC2 = BC2 - AB2 = 102 - 62 = 64
=> AC = 8 (cm)
Ta có: t/giác HBA đồng dạng t/giác ABC
=> HB/AB = AH/AC = AB/BC
hay HB/6 = AH/8 = 6/10 = 3/5
=> \(\hept{\begin{cases}HB=\frac{3}{5}.6=3,6\left(cm\right)\\AH=\frac{3}{5}.8=4,8\left(cm\right)\end{cases}}\)
c) Xét tứ giác AIHK có \(\widehat{A}=\widehat{AKH}=\widehat{AIH}=90^0\)
=> AIHK là HCN => \(\widehat{AIK}=\widehat{AHK}\)(cùng = \(\widehat{IKH}\)) (1)
Ta có: \(\widehat{AHK}+\widehat{KHC}=90^0\)(phụ nhau)
\(\widehat{KHC}+\widehat{C}=90^0\)(phụ nhau)
=> \(\widehat{AHK}=\widehat{C}\) (2)
Từ (1) và )2) => \(\widehat{AIK}=\widehat{C}\)
Xét t/giác AKI và t/giác ABC
có: \(\widehat{A}=90^0\): chung
\(\widehat{AIK}=\widehat{C}\)(cmt)
=> t/giác AKI đồng dạng t/giác ABC
=> AI/AC = AK/AB => AI.AB = AK.AC
d) Do AD là đường p/giác của t/giác ABC => \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{BC-DC}{DC}=\frac{BC}{DC}-1\)
<=> \(\frac{10}{DC}-1=\frac{6}{8}\) <=> \(\frac{10}{DC}=\frac{7}{4}\) <=> \(DC=\frac{40}{7}\)(cm)
=> BD = 10 - 40/7 = 30/7 (cm)
DE là đường p/giác của t/giác ABD => \(\frac{AD}{BD}=\frac{AE}{EB}\)(t/c đg p/giác)
DF là đường p/giác của t/giác ADC => \(\frac{DC}{AD}=\frac{FC}{AF}\)
Khi đó: \(\frac{EA}{EB}\cdot\frac{DB}{DC}\cdot\frac{FC}{FA}=\frac{AD}{DB}\cdot\frac{AB}{AC}\cdot\frac{DC}{AD}=\frac{AB\cdot DC}{BD.AC}=\frac{6\cdot\frac{40}{7}}{8\cdot\frac{30}{7}}=1\) (ĐPCM)

a,vì tam giác abd = tam giác acb ---> tam giác abd đồng dạng vs tam giác acb

A B C D H m n
Gọi tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng \(\frac{m}{n}\)
Kẻ \(AH\perp BC\)
Ta có: \(S_{ABD}=\frac{1}{2}AH.BD\)và \(S_{ADC}=\frac{1}{2}AH.DC\)
\(\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}\)
Mặt khác: AD là đường phân giác của tam giác ABC
\(\Rightarrow\frac{BD}{DC}=\frac{AB}{AC}=\frac{m}{n}\)
Gọi DM và DN lần lượt là đường cao của tam giác ADB và tam giác ACD
Xét tam giác ADB và tam giác ACD có :
góc BAD=góc DAC (gt)
AD chung
góc AMD = góc AND ( = 90 độ )
=> Tam giác ADB = tam giác ACD ( ch-gn)
=> DM=DN
TA có :
Stam giác ABD/Stam giác ADC
=(1/2.DM.AB)/(1/2.DN.AC)
=(1/2.DM.AB)/(1/2.DM.AC)=AB/AC=m/n (đpcm)
Như vầy cũng được mà trên mạng nó có mà sao bạn không chịu tìm nhỉ ???
Từ A kẻ đường cao AH, H thuộc BC.
Xét \(\Delta ABC:\) AD là đường phân giác (gt).
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}\) (Tính chất đường phân giác).
Ta có:
\(S_{\Delta ABD}=\dfrac{1}{2}.AH.BD.\\ S_{\Delta ACD}=\dfrac{1}{2}.AH.DC.\\ \Rightarrow\dfrac{S_{\Delta ABD}}{S_{\Delta ACD}}=\dfrac{\dfrac{1}{2}.AH.BD}{\dfrac{1}{2}.AH.DC}=\dfrac{BD}{DC}.\)
Mà \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\left(cmt\right).\)
\(\Rightarrow\dfrac{S_{\Delta ABD}}{S_{\Delta ACD}}=\dfrac{AB}{AC}.\)