Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
b: ΔABD=ΔAED
=>góc AED=góc ABD=90 độ
c: Xét ΔAEF vuông tại A và ΔABC vuông tại B có
AE=AB
góc EAF chung
=>ΔAEF=ΔABC
=>AF=AC
d: DB=DE
mà DE<DC
nên DB<DC

A B C D E
a, xét tam giác ABD và tam giác AED có AB = AE (Gt)
AD chung
^BAD = ^EAD do AD Là pg của ^BAC (Gt)
=> tg ABD = tg AED (c-g-c)
=> BD = ED (Đn)
=> tam giác BED cân tại D (đn)
b, tg ABC có AD là pg => DC/AC = DB/AB (tc)
có AC > AB (GT)
=> DC > DB
Bài làm
a) Xét tam giác ADB và tam giác ADE có:
AB = AE ( gt )
\(\widehat{BAD}=\widehat{EAD}\)( Do AD phân giác )
AD chung
=> Tam giác ADB = tam giác ADE ( c.g.c )
=> BD = DE
=> Tam giác DBE cân ở D.
b) Kẻ BH là tia đối của tia BA.
Xét tam giác BAC có: \(\widehat{CBH}=\widehat{BAC}+\widehat{ACB}\)
=> \(\widehat{ACB}< \widehat{CBH}\)
Hay \(\widehat{DCE}< \widehat{CBH}\) (1)
Vì tam giác ADB = tam giác ADE ( cmt )
=> \(\widehat{ABD}=\widehat{AED}\)
Mà \(\widehat{ABD}+\widehat{DBH}=180^0\)( Hai góc kề bù )
\(\widehat{AED}+\widehat{DEC}=180^0\)( Hai góc kề bù )
=> \(\widehat{DBH}=\widehat{DEC}\)
Hay \(\widehat{CBH}=\widehat{DEC}\) (2)
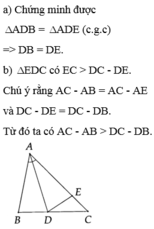
Từ (1) và (2) => \(\widehat{DCE}< \widehat{DEC}\)
Xét tam giác DEC có:
\(\widehat{DCE}< \widehat{DEC}\)
=> DE < DC ( Qua hệ giữ cạnh và góc đối diện )
Mà DE = BD ( cmt )
=> BD < DC
Hay DC > DB ( đpcm )

a)xet tam giac abd va tam giac aed co
ab=ae
ad la canh chunggoc bad = goc ead
=>tam giác abd = ead
b)gọi i là giao điểm của ad và be
xét tam giác abi và tam giác aei có :
ab=ae
ad là cạnh chung
goc bai = góc eai
=> tam giác abi= tâm giác aei
=>ib=ie =>ad là đường trung trực của be
cho mk 3 đi mk giải tiếp cho, bài nay mk vừa mới kiểm tra
mk giải tiếp nè
theo câu a,b=>góc dbf= góc dec (kề bù do góc abd= aed)
xét tam giác bfd và ecd có
góc dbf= góc dec
bd=ed
bdf=edc
=> tam giác dbf= tam giác ecd
k cho mk đi.mk hứa mk tl hết cho mà

A B C D E F 1 2
a) Vì AD là tia phân giác của tam giác ABC => \(\widehat{A_1}=\widehat{A_2}\)
Xét tam giác ABD và tam giác ADE có : \(\hept{\begin{cases}AE=AB\left(GT\right)\\\widehat{A_1}=\widehat{A_2}\left(cmt\right)\\Chung\end{cases}AD=>}\)Tam giác ADB=Tam giác ADE (c-g-c) (đpcm)
b) Vì tam giác ADB= tam giác ADE ( cmt phần a) => DB = DE ( cạnh tương ứng ) => D thuộc đường trung trực cuae BE (1)
Vì AB=AE(GT) => A thuộc đường trung trực của BE (2).Từ (1);(2)=> AD là đường trung trực của BE (đpcm)
c)Vì tam giác ADB=tam giác ADE ( cmt phần ) => \(\widehat{ABD=}\widehat{AED}\)(góc tương ứng) và \(\widehat{ADB}=\widehat{ADE}\)(góc tương ứng )
Vì\(\widehat{FBD}\)là góc ngoài tam giác ABD => \(\widehat{FBD}=\widehat{ABD}+\widehat{ADB}\)
Vì \(\widehat{DEC}\)là góc ngoài tam giác ADE => \(\widehat{DEC}=\widehat{ADE}+\widehat{AED}\)
\(=>\widehat{FBD}=\widehat{DEC}\)
Xét tam giác BDF và tam giác ECD có : \(\hept{\begin{cases}\widehat{FBD}=\widehat{DEC}\\BD=CE\left(cmt\right)\\\widehat{BDF}=\widehat{ECD}\end{cases}}\)=> Tam giác BDF = Tam giác ECD (đpcm)
=> \(\hept{\begin{cases}CE=BF\\\widehat{C}=\widehat{BFD}\end{cases}}\)
Vì DE = DB(cmt phần b) => Tam giác DBE cân tại D => \(\widehat{DBE}=\widehat{DEB}\)
Mà \(\widehat{FBD}=\widehat{CED}\)(cmt)=> \(\widehat{FBD}+\widehat{DBE}=\widehat{CED}+\widehat{DEB}=>\widehat{FBE}=\widehat{CEB}\)
Xét tam giác BCE và tam giác EFB có : \(\hept{\begin{cases}\widehat{BFD}=\widehat{ECD}\left(cmt\right)\\BF=CE\left(cmt\right)\\\widehat{FBE}=\widehat{CEB}\end{cases}}\)=> Tam giác BCE = Tam giác EFB (g-c-g) (đpcm)
d) Vì \(\widehat{FBD}\)là góc ngoài của tam giác ABC => \(\widehat{FBD}=\widehat{ABC}+\widehat{ACB}=>\widehat{FBD}>\widehat{ACB}\)
Mà \(\widehat{FCB}=\widehat{CED}=>\widehat{CED}>\widehat{ACB}\)=> Tam giác DEC có DC>DE
mà DE=DB( cmt phần b)=> DB <DC