Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để giải bài toán, ta sẽ sử dụng các định lý trong hình học tam giác. a/ Để tính HB và HC, ta cần tìm độ dài đường cao AH trước. Với thông tin AH.AC = 3.5 và AC = 15cm, ta có thể tính được AH: AH = (AH.AC)/AC = (3.5)/(15) = 0.2333 cm Tiếp theo, ta xét tam giác ABC với tam giác ABC. góc B và đường cao AH. Áp dụng định lý Pythagoras, ta có công thức: AB^2 = AH^2 + BH^2 Với độ dài AB = 15cm, ta có: 15^2 = 0,2333^2 + BH^2 225 = 0,0544 + BH^2 BH^2 = 224,9456 BH ≈ 14,998 cm Tương tự, ta có: HC ≈ 0,2333 cm Vậy HB ≈ 14,998 cm và HC ≈ 0,2333 cm. b/ Để chứng minh AH^3 = BC.BE.CF, ta sẽ sử dụng các tỷ lệ trong tam giác tương đồng. Kiểm định tam giác AHB và tam giác AFC, ta có: AH/AF = HB/FC 0.2333/AF = 14.998/(15 - FC) Tương tự, xét tam giác AHC và tam giác AEB, ta có: AH/AE = HC/EB 0.2333/AE = 0.2333/(15 - EB ) Từ hai tỷ lệ trên, ta có: AF/(15 - FC) = AE/(15 - EB) Nhân cả hai quan sát với (15 - FC)(15 - EB), ta có: AF(15 - EB) = AE(15 - FC) Vậy ta có BC.BE.CF = AF(15 - EB) = AE(15 - FC) = AH^2. Do đó, AH^3 = BC.BE.CF.
a: Sửa đề: AH/AC=3/5
Xét ΔAHC vuông tại H có sin C=AH/AC=3/5
Xét ΔABC vuông tại A có sin C=AB/BC
=>15/BC=3/5
=>BC=25(cm)
=>\(AC=\sqrt{25^2-15^2}=20\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên BH*BC=BA^2; CH*CB=CA^2
=>BH=15^2/25=9cm; CH=20^2/25=16cm
b: BC*BE*CF
=BC*BH^2/BA*CH^2/CA
=AH^4/AH
=AH^3

Đề đúng là: \(\dfrac{AH}{AC}=\dfrac{3}{5}\). Bạn tự vẽ hình nhé.
(a) Theo đề: \(\dfrac{AH}{AC}=\dfrac{3}{5}\Leftrightarrow AC=\dfrac{5}{3}AH\)
Ta có: \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Leftrightarrow BC^2=15^2+\left(\dfrac{5}{3}AH\right)^2\Rightarrow BC=\sqrt{225+\dfrac{25}{9}AH^2}\)
Lại có: \(AB^2=BC.HB\Leftrightarrow HB=\dfrac{AB^2}{BC}=\dfrac{15^2}{\sqrt{225+\dfrac{25}{9}AH^2}}\)
Ta cũng có: \(AH^2=HB.HC=HB\left(BC-HB\right)=BC.HB-HB^2\)
\(\Leftrightarrow AH^2=\sqrt{225+\dfrac{25}{9}AH^2}\cdot\dfrac{15^2}{\sqrt{225+\dfrac{25}{9}AH^2}}-\left(\dfrac{15^2}{\sqrt{225+\dfrac{25}{9}AH^2}}\right)^2\)
\(=15^2-\dfrac{15^4}{225+\dfrac{25}{9}AH^2}\)
\(\Rightarrow AH=12\left(cm\right)\)
Thay vào tính được: \(HB=9\left(cm\right);BC=25\left(cm\right)\)
\(\Rightarrow HC=BC-HB=25-9=16\left(cm\right)\)
(b) Xét \(\Delta AHB\) vuông tại \(H:BE.AB=HB^2\Leftrightarrow BE=\dfrac{HB^2}{AB}\)
Tương tự, \(\Delta AHC\) vuông tại \(H:CF.AC=HC^2\Leftrightarrow CF=\dfrac{HC^2}{AC}\)
Ta có: \(BC.BE.CF=\left(\dfrac{AB.AC}{AH}\right)\cdot\dfrac{HB^2}{AB}\cdot\dfrac{HC^2}{AC}\)
\(=\dfrac{HB^2.HC^2}{AH}=\dfrac{\left(HB.HC\right)^2}{AH}=\dfrac{\left(AH^2\right)^2}{AH}=AH^3\left(đpcm\right)\)


A B C H M E F N I
A. Ta có \(\frac{AH}{AC}=\frac{3}{5}\Rightarrow AC=\frac{5}{3}AH\)
Theo hệ thức lượng trong tam giác vuông ta có \(AB^2=BC^2-AC^2=\frac{AB^2AC^2}{AH^2}-AC^2\Rightarrow15^2=\frac{15^2.\frac{25}{9}AH^2}{AH^2}-AC^2\)
\(\Rightarrow AC^2=400\Rightarrow AC=20\left(cm\right)\Rightarrow BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(\Rightarrow HB=\frac{AB^2}{BC}=9\left(cm\right);HC=BC-BH=25-9=16\left(cm\right)\)
b.Vì E;F là hình chiếu của H lên AB;AC \(\Rightarrow\widehat{E}=\widehat{F}=\widehat{A}=90^0\Rightarrow AEHF\)là hình chữ nhật
c. Gỉa sử \(AM⊥EF\)\(\Rightarrow\)ta phải chứng minh M là trung điểm BC
Gọi I là giao điểm của EF và AH ; N là giao của EF và AM
Xét tam giác AIN và tam giác AHM
có \(\hept{\begin{cases}\widehat{A}chung\\\widehat{N}=\widehat{H}=90^0\end{cases}\Rightarrow\Delta AIN~\Delta AHM\left(g-g\right)\Rightarrow\widehat{AIN}=\widehat{AMH}\left(1\right)}\)
Xét tam giác AEF và tam giác ACB có \(\hept{\begin{cases}\widehat{A}=90^0chung\\\widehat{C}=\widehat{E}\left(+\widehat{B}=90^0\right)\end{cases}\Rightarrow\Delta AEF~\Delta ACB\left(g-g\right)\Rightarrow\widehat{AFE}=\widehat{B}\left(2\right)}\)
Vì AEHF là hình chữ nhật nên \(\widehat{IFA}=\widehat{IAF}\left(3\right)\)
Lại có \(\widehat{AIF}=180^0-2.\widehat{IFA}\)
Từ (1) ;(2) và (3) \(\Rightarrow\widehat{AMB}=180^0-2.\widehat{B}\Rightarrow\Delta AMB\)cân tại M \(\Rightarrow MA=MB\)
Tương tự chứng minh được \(MA=MC\)\(\Rightarrow M\)là trung điểm BC
Vậy trung tuyến AM vuông góc với EF
d. Gỉa sử tam giác ABC vuông cân \(\Leftrightarrow AB=AC\Rightarrow S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}AB^2\left(4\right)\)
\(\Delta ABC\)vuông cân \(\Leftrightarrow AE=AF\Rightarrow S_{AEHF}=AE.AF=AE^2=\frac{1}{4}AB^2\Rightarrow2S_{AEHF}=\frac{1}{2}AB^2\left(5\right)\)
Từ (4) và (5) ta có \(S_{ABC}=2S_{AEHF}\)đúng với giả thiết ban đầu
Vậy giả sử \(S_{ABC}=2S_{AEHF}\)thì tam giác ABC vuông cân

a, xét \(\Delta ABC\) vuông tại A áp dụng hệ thức lượng\(=>AC^2=CH.BC=>HC=\dfrac{AC^2}{BC}=\dfrac{12^2}{15}=9,6cm\)
\(=>HB=BC-HC=15-9,6=5,4cm\)
áp dụng Pytago trong \(\Delta AHC\) vuông tại H
\(=>HA=\sqrt{AC^2-HC^2}=\sqrt{12^2-9,6^2}=7,2cm\)
\(b,\) do E,F là hình chiếu vuông góc của H lần lượt lên AB, AC
\(=>\left\{{}\begin{matrix}EH\perp AB\\HF\perp AC\end{matrix}\right.\) mà \(\Delta AHB\) và \(\Delta AHC\) lần lượt vuông góc tại H
theo hệ thức lượng
\(=>\left\{{}\begin{matrix}AH^2=AE.AB\\AH^2=AF.AC\end{matrix}\right.\)=>\(AE.AB=AF.AC\)
c, do E,F là hình chiếu vuông góc của H lần lượt lên AB, AC
=> tứ giác EHFA là hình chữ nhật\(=>AE=HF< =>HF^2=AE^2\)
áp dụng pytago trong \(\Delta EHA\) vuông tại E
\(=>HE^2+AE^2=AH^2< =>HE^2+HF^2=AH^2\)(1)
theo hệ thức lượng trong tam giác ABC vuông tại A đường cao AH
\(=>AH^2=HB.HC\left(2\right)\)
(1)(2)=>\(HE^2+HF^2=HB.HC\)

a) Ta có: \(\dfrac{HB}{HC}=\dfrac{HB.HC}{HC^2}=\dfrac{HA^2}{HC^2}=\left(\dfrac{HA}{HC}\right)^2\)
Xét \(\Delta AHC\) và \(\Delta BAC:\) Ta có: \(\left\{{}\begin{matrix}\angle AHC=\angle BAC=90\\\angle ACBchung\end{matrix}\right.\)
\(\Rightarrow\Delta AHC\sim\Delta BAC\left(g-g\right)\Rightarrow\dfrac{HA}{HC}=\dfrac{AB}{AC}\)
\(\Rightarrow\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2=\dfrac{c^2}{b^2}\)
b) tham khảo ở đây:https://hoc24.vn/cau-hoi/cho-dabc-vuong-tai-a-duong-cao-ah-goi-e-f-lan-luot-la-cac-hinh-chieu-cua-h-tren-ab-va-ac-cmra-aeabaf.1150118751274
a) Áp dụng hệ thức lượng trong tam giác vuông có:
\(AB^2=BH.BC\)
\(AC^2=CH.CB\)
\(\Rightarrow\dfrac{BH}{CH}=\dfrac{AB^2}{AC^2}=\dfrac{c^2}{b^2}\)
b) Áp dụng hệ thức lượng trong tam giác vuông có:
\(BH^2=BE.BA\)
\(CH^2=CF.CA\)
\(\Rightarrow\dfrac{BH^2}{CH^2}=\dfrac{BE}{CF}.\dfrac{BA}{CA}\)\(\Leftrightarrow\dfrac{c^4}{b^4}=\dfrac{BE}{CF}.\dfrac{c}{b}\)
\(\Leftrightarrow\dfrac{BE}{CF}=\dfrac{c^3}{b^3}\)

a: \(AH\cdot BC=AB\cdot AC\)
nên AH/AC=AB/BC=3/5
=>BC=25cm
\(AC=\sqrt{25^2-15^2}=20\left(cm\right)\)
\(HB=\dfrac{225}{25}=9\left(cm\right)\)
HC=25-9=16cm
b: \(BC\cdot BE\cdot CF\)
\(=\dfrac{BH^2}{AB}\cdot\dfrac{CH^2}{AC}\cdot\dfrac{AB\cdot AC}{AH}\)
\(=\dfrac{AH^4}{AH}=AH^3\)

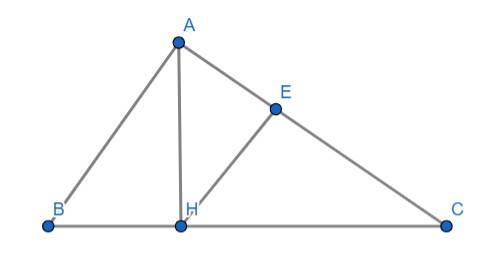
Ta có:
\(\left\{{}\begin{matrix}AB^2=BC\cdot BH\Rightarrow AB=\sqrt{BC\cdot BH}=\sqrt{\left(8+2\right)\cdot2}=2\sqrt{5}\left(cm\right)\\AC^2=BC\cdot CH\Rightarrow AC=\sqrt{BC\cdot CH}=\sqrt{\left(8+2\right)\cdot8}=4\sqrt{5}\left(cn\right)\end{matrix}\right.\)
\(BC\cdot AH=AB\cdot AC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{2\sqrt{5}\cdot4\sqrt{5}}{2+8}=4\left(cm\right)\)
\(sinC=\dfrac{AB}{BC}=\dfrac{2\sqrt{5}}{10}\Rightarrow\widehat{C}\approx27^o\)