

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

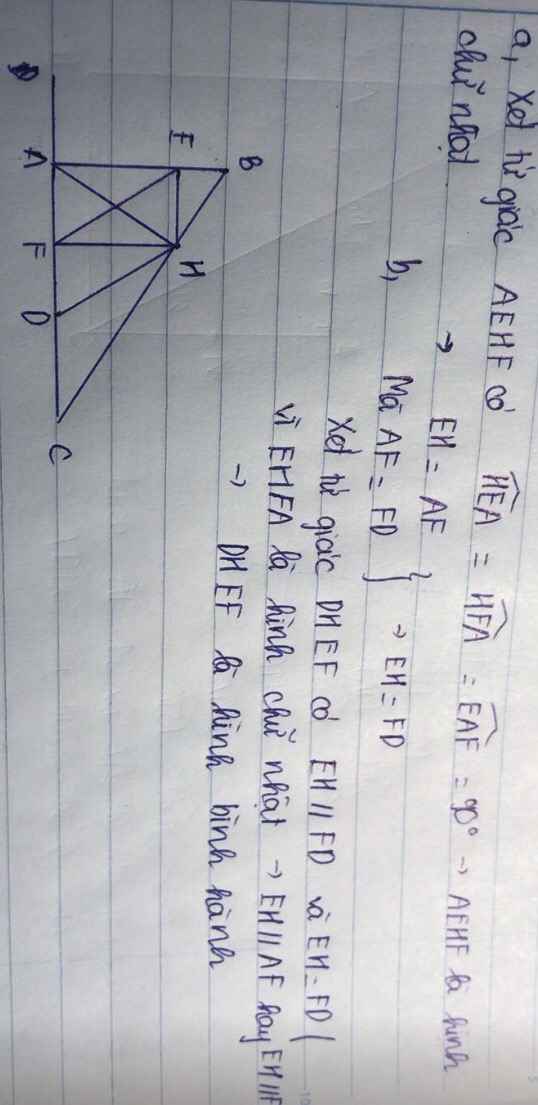


a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
b: Xét tứ giác DHEF có
HE//DF
HE=DF
Do đó: DHEF là hình bình hành

a: Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật
b: FA=FD
FA=HE
=>HE=FD
Xét tứ giác HEFD có
HE//FD
HE=FD
=>HEFD là hình bình hành
c: Sửa đề: MP vuông góc AB
M đối xứng G qua AB
=>MG vuông góc AB tại trung điểm của MG
=>MG vuông góc AB tại P và P là trung điểm của MG
XétΔABC có
M là trung điểm của BC
MP//AC
=>P là trung điểm của AB
Xét tứ giác AMBG có
P là trung điểm chung của AB và MG
MA=MB
=>AMBG là hình thoi
M đối xứng K qua AC
=>MK vuông góc AC tại trung điểm của MK
=>Q là trung điểm của MK
Xét ΔABC có
M là trung điểm của BC
MQ//AB
=>Q là trung điểm của AC
Xét tứ giác AMCK có
Q là trung điểm chung của AC và MK
MA=MC
=>AMCK là hình thoi

a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật

a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật

xin lỗi anh(chị) em mới lớp 6 không giải đc
thật lòng xin lỗi :(((((
((((((((🙄)))))))))___________bn ghi như mình đi thì bn sẽ có cái nịt 👉👈!!!

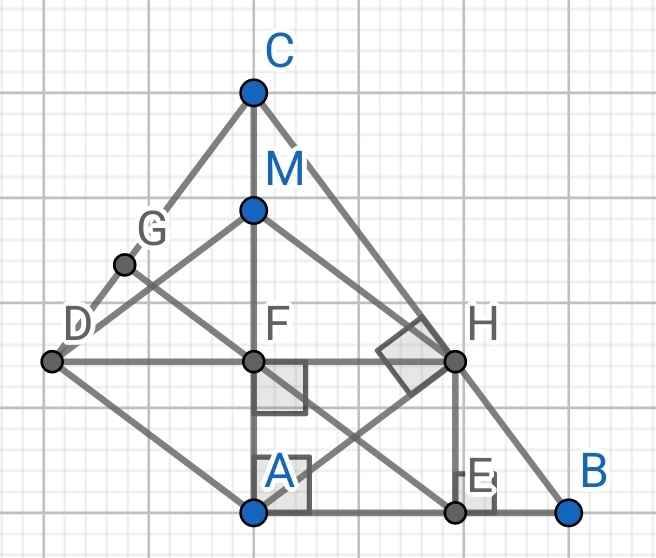 a) Do HE ⊥ AB (gt)
a) Do HE ⊥ AB (gt)
⇒ ∠AEH = 90⁰
Do HF ⊥ AC (gt)
⇒ ∠AFH = 90⁰
Do ∆ABC vuông tại A (gt)
⇒ ∠EAF = 90⁰
Tứ giác AEHF có:
∠AEH = ∠AFH = ∠EAF = 90⁰
⇒ AEHF là hình chữ nhật
b) Do AEHF là hình chữ nhật (cmt)
⇒ HE = AF
Mà AF = FM (do A và M đối xứng qua F)
⇒ HE = FM
Do AEHF là hình chữ nhật (cmt)
⇒ HE // AF
⇒ HE // FM
Tứ giác EFMH có:
HE // FM (cmt)
HE = FM (cmt)
⇒ EFMH là hình bình hành
c) Do A và M đối xứng qua F (gt)
⇒ F là trung điểm của AM
Do D và H đối xứng qua F (gt)
⇒ F là trung điểm của DH
Do HF ⊥ AC (gt)
⇒ HD ⊥ AM
Tứ giác AHMD có:
F là trung điểm của AM (cmt)
F là trung điểm của DH (cmt)
⇒ AHMD là hình bình hành
Mà HD ⊥ AM (cmt)
⇒ AHMD là hình chữ thoi
⇒ AD // MH
Do EFMH là hình bình hành (cmt)
⇒ EF // MH
Mà AD // MH
⇒ EF // AD
Do ADMH là hình thoi (cmt)
⇒ AM là tia phân giác của ∠DAH
⇒ ∠DAM = ∠HAM
⇒ ∠DAC = ∠HAC
Do ADMH là hình thoi
⇒ AD = AH
Xét ∆ADC và ∆AHC có:
AD = AH (cmt)
∠DAC = ∠HAC (cmt)
AC là cạnh chung
⇒ ∆ADC = ∆AHC (c-g-c)
⇒ ∠ADC = ∠AHC = 90⁰ (hai góc tương ứng)
⇒ AD ⊥ DC
Mà EF // AD (cmt)
⇒ EF ⊥ DC