Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì BE vuông góc với AC tại E (E ϵAC) ⇒ góc BEC =\(90^0\)
Vì CF vuông góc với AB tại F (F ϵ AB) ⇒ góc BFC =\(90^0\)
xét tứ giác BCEF có ;
góc BEC+BFC=\(90^0+90^0=180^0\)
mà hai góc ở vị trí kề nhau
⇒tứ giác BCEF là tgnt hay A,C,E,F cùng nằm trên một đtròn
b,

a)Nối F với D : E với D ta có:
Xét tam giác FBC ta có
D là trung điểm BC(1)
Góc BFC=90 (2)
Từ (1)(2)=>FD là trung tuyến của tam giác FBC
=>BD=CD=DF(*)
Chứng minh tương tự tam giác EBC
=>DE=DC=DB(**)
Từ (*)(**)=>BD=CD=DF=DE=(1/2BC)
=>B;F;E;C thuộc đừng tròn
=>D là tâm của đường tròn
B) Do B;H;E nằm trên cùng 1 đừng thẳng => H ko thuộc đừng tròn
=>B;H;E;c ko thuộc đừng tròn

a: góc AEH=góc AFH=90 độ
=>AEHF nội tiếp đường tròn tâm I, I là trung điểm của AH
b: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp đường tròn đường kính BC
=>O là trung điểm của BC
c: góc IEO=góc IEH+góc OEH
=góc IHE+góc OBE
=góc OBE+góc OCE=90 độ
=>IE là tiếp tuyến của (O)
d: IE=IF
OE=OF
=>IO là trung trực của EF

a) Tự làm nhá
b) +) CM \(\Delta ADC~\Delta HDE\left(g-g\right)\)
=> DA.HE=DH.AC
+) \(\Delta BAD\)cân\(=>\widehat{BAD}=90^0-\frac{1}{2}\widehat{B}=\widehat{CAD}\)
mà \(\widehat{CAD}=\widehat{B}\)
=> AD là tia phân giác góc HAC => Góc HAE = góc CAE => cung HE= cung CE => cạnh HE = cạnh CE => tam giác cân (dpcm)
3) Xét \(\Delta MNP\)zuông tại M ngoại tiếp đươg tròn tâm I , bán kính r , tiếp xúc các cạnhMN , MP,NP thứ tự tại D, E ,F
ta có \(\widehat{IEM}=\widehat{IDM}=\widehat{DME}=90\);ID =IE=r
=> tứ giác IEMD là hình zuông
=> MD=ME=r
Có ND=NF,PE =PF( các tia tiếp tuyến cắt nhau)
=> MN+MP-NP=MD+ND+ME+PE-NF-PF=MD+ME=2r
tam giác ABH zuông tại H có \(\hept{\begin{cases}R_1=\frac{AH+BH-AB}{2}\\\end{cases}}\)
Tam giác ACH zuông tại H có \(R_2=\frac{AH+CH-AC}{2}\)
tam giác ABC zuông tại A có \(R_3=\frac{AB+AC-BC}{2}\)
\(=>R_1+R_2+R_3=AH\)
ta có \(AH\le AO=\frac{6}{2}=3cm\)
dấu = xảy ra khi H trung O
=> A là điểm chính giữa cung BC
Nguồn : https://qanda.ai/vi/solutions/npWTTopujG-Cho-n%E1%BB%ADa-%C4%91%C6%B0ong-tr%C3%B2n-t%C3%A2m-O-d%C6%B0%E1%BB%9Dng-k%C3%ADnh-BC6cm-Tr%C3%AAn-n%E1%BB%ADa-%C4%91%C6%B0%E1%BB%9Dng-tr%C3%B2n

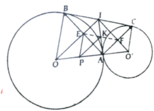
a, Chứng minh tứ giác AEIF là hình chữ nhật và K là trung điểm AI
b, Có IE.IO = I B 2 = B C 2 4 và IF.IO' = I C 2 = B C 2 4
=> 2.(IE.IO+IF.IO') = A B 2 + A C 2
c, PK Là đường trung bình của ∆OAI và là trung trực của EA
Ta có ∆PEK = ∆PAK nên P E K ^ = P A K ^
Vậy P E K ^ = 90 0 => đpcm
d, ∆ABC:∆IOO’ => S A B C S I O O ' = B C O O ' 2 => S A B C = S I O O ' . B C 2 O O ' 2
mà BC = 2AI'; OO' = 2a; S O I O ' = 1 2 . 2 a . I A = a . I A => S A B C = I A 2 a
I A 2 = R R ' ⩽ R + R ' 2 2 = a 2 => IA lớn nhất bằng a khi R=R’

Vì BE vuông góc với AC tại E (E ϵAC) ⇒ góc BEC =900900
Vì CF vuông góc với AB tại F (F ϵ AB) ⇒ góc BFC =900900
xét tứ giác BCEF có ;
góc BEC+BFC=900+900=1800900+900=1800
mà hai góc ở vị trí kề nhau
⇒tứ giác BCEF là tgnt hay A,C,E,F cùng nằm trên một đtròn
b,