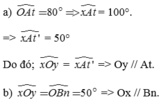Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải
x O y A t m B n
a.
\(\widehat{OAt }+\widehat{ tAx }=180^o\) (2 góc kề bù)
\(100^o+\widehat{tAx}=180^o\)
\(\widehat{tAx}=80^o\)
Am là tia phân giác của \(\widehat{tAx}\)
=> \(\widehat{tAm}\) = \(\widehat{mAx}\) = \(\frac{\widehat{tAx}}{2}=\frac{80^o}{2}=40^o\)
mà \(\widehat{xOy}=40^o\)
=> \(\widehat{xOy}=\widehat{xAm}\)
mà 2 góc này ở vị trí đồng vị
=> Oy // Am
b.
Bn // Ox
<=> \(\widehat{nBO}=\widehat{xOB}\) (2 góc so le trong)
mà \(\widehat{xOB}=40^o\)
=>\(\widehat{nBO}=40^o\)

O y x A t m n
a) Ta có: \(\widehat{xOy}+\widehat{OAt}=120^0+60^0=180^0\)
Mà hai góc ở vị trí: trong cùng phía bù nhau
Nên At // Oy
b) On là tia phân giác của góc xOy \(\Rightarrow\widehat{yOn}=\widehat{xOn}=\frac{\widehat{xOy}}{2}=\frac{120^0}{2}=60^0\)
Vì At // Oy => \(\widehat{xAt}=\widehat{xOy}=120^0\) (đồng vị)
Am là tia phân giác của góc xAt \(\Rightarrow\widehat{xAm}=\widehat{tAm}=\frac{\widehat{xAt}}{2}=\frac{120^0}{2}=60^0\)
Ta thấy \(\widehat{xAm}=\widehat{xOn}=60^0\)
Mà hai góc này ở vị trí đồng vị
=> On // Am

Bạn tự vẽ hình nha![]()
a.
OAt + tAx = 1800 (2 góc kề bù)
1000 + tAx = 1800
tAx = 1800 - 1000
tAx = 800
Am là tia phân giác của tAx
=> tAm = mAx = \(\frac{tAx}{2}=\frac{80^0}{2}\) = 400
mà xOy = 400
=> xOy = xAm
mà 2 góc này ở vị trí đồng vị
=> Am // Oy
b.
Bn // Ox
<=> nBO = xOB (2 góc so le trong)
mà xOB = 400
=> nBO = 400
Chúc bạn học tốt![]()

Hình bạn tự vẽ nha!
Bài 2:
a) Ta có: \(\widehat{OAt}+\widehat{tAx}=180^0\) (vì 2 góc kề bù)
=> \(100^0+\widehat{tAx}=180^0\)
=> \(\widehat{tAx}=180^0-100^0\)
=> \(\widehat{tAx}=80^0.\)
Vì \(Am\) là tia phân giác của \(\widehat{tAx}\left(gt\right)\)
=> \(\widehat{tAm}=\widehat{mAx}=\frac{\widehat{tAx}}{2}=\frac{80^0}{2}=40^0.\)
Mà \(\widehat{xOy}=40^0\left(gt\right)\)
=> \(\widehat{xOy}=\widehat{mAx}\)
Mà 2 góc này nằm ở vị trí đồng vị.
=> \(Am\) // \(Oy.\)
b) Ta có: \(Bn\) // \(Ox\left(gt\right)\)
=> \(\widehat{nBO}=\widehat{xOB}\) (vì 2 góc so le trong)
Mà \(\widehat{xOB}=40^0.\)
=> \(\widehat{nBO}=40^0.\)
Vậy \(\widehat{nBO}=40^0.\)
Chúc bạn học tốt!