Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) \(\left|\overrightarrow{a}+\overrightarrow{b}\right|=\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|\) khi vectơ a và vectơ b cùng hướng

Bài này sử dụng bất đẳng thức tam giác
Đặt vectơ AB = a vectơ BC = b
Ta có: \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\) hay \(\left|\overrightarrow{a}+\overrightarrow{b}\right|=\overrightarrow{AC}\)
Ta lại có: \(AB+BC\ge AC\) ( bđt tam giác )
Từ 2 điều trên ta suy ra đpcm \(\left|\overrightarrow{a}+\overrightarrow{b}\right|\le\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|\)

\(\left(\overrightarrow{a}+\overrightarrow{b}\right)^2=\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)\)\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2+2\overrightarrow{a}\overrightarrow{b}\).
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)\)\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2-2\overrightarrow{a}\overrightarrow{b}\).
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left|\overrightarrow{a}\right|^2+\overrightarrow{a}\overrightarrow{b}-\overrightarrow{a}\overrightarrow{b}+\left|\overrightarrow{b}\right|^2\)\(=\left|\overrightarrow{a}\right|^2-\left|\overrightarrow{b}\right|^2\).

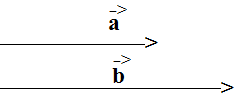
giả sử tam giác ABC \(\overrightarrow{BC}\)=\(\overrightarrow{a}\) \(\overrightarrow{AC}\)= \(\overrightarrow{b}\) \(\overrightarrow{AB}\)=\(\overrightarrow{c}\)
theo đề ta có
BC-AC< AB < BC+AC