Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ĐKXĐ: \(\left\{{}\begin{matrix}a>=0\\a\ne1\end{matrix}\right.\)
b: Sửa đề: \(C=\left[1:\left(1-\dfrac{\sqrt{a}}{1+\sqrt{a}}\right)\right]\cdot\left[\dfrac{1}{\sqrt{a}-1}-\dfrac{2\sqrt{a}}{\left(a+1\right)\left(\sqrt{a}-1\right)}\right]\)
\(=\left[1:\dfrac{a+\sqrt{1}-\sqrt{a}}{\sqrt{a}+1}\right]\cdot\left[\dfrac{a+1-2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(a+1\right)}\right]\)
\(=\dfrac{\sqrt{a}+1}{1}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)\left(a+1\right)}\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{a+1}=\dfrac{a-1}{a+1}\)
c: Để C là số nguyên thì \(a-1⋮a+1\)
=>\(a+1-2⋮a+1\)
=>\(-2⋮a+1\)
=>\(a+1\in\left\{1;-1;2;-2\right\}\)
=>\(a\in\left\{0;-2;1;-3\right\}\)
Kết hợp ĐKXĐ, ta được: a=0

a) ĐKXĐ: \(\left\{{}\begin{matrix}a>0\\a\ne1\end{matrix}\right.\)
b) Ta có: \(M=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)\left(\dfrac{a-\sqrt{a}}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}}{\sqrt{a}-1}\right)\)
\(=\dfrac{a-1}{2\sqrt{a}}\cdot\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)^2-\sqrt{a}\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{\sqrt{a}\left[\left(\sqrt{a}-1\right)^2-\left(\sqrt{a}+1\right)^2\right]}{2\sqrt{a}}\)
\(=\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{2}\)
\(=\dfrac{-4\sqrt{a}}{2}=-2\sqrt{a}\)
c) Để M=-4 thì \(-2\sqrt{a}=-4\)
\(\Leftrightarrow\sqrt{a}=2\)
hay a=4(thỏa ĐK)

Lời giải:
a) ĐKXĐ: \(a>0; a\neq 1\)
\(M=\left(\frac{\sqrt{a}}{2}-\frac{1}{2\sqrt{a}}\right)\left(\frac{a-\sqrt{a}}{\sqrt{a}+1}-\frac{a+\sqrt{a}}{\sqrt{a}-1}\right)\)
\(=\frac{a-1}{2\sqrt{a}}.\frac{(a-\sqrt{a})(\sqrt{a}-1)-(a+\sqrt{a})(\sqrt{a}+1)}{(\sqrt{a}+1)(\sqrt{a}-1)}\)
\(=\frac{a-1}{2\sqrt{a}}.\sqrt{a}.\frac{(\sqrt{a}-1)^2-(\sqrt{a}+1)^2}{a-1}\)
\(=\frac{(\sqrt{a}-1)^2-(\sqrt{a}+1)^2}{2}=\frac{a+1-2\sqrt{a}-(a+1+2\sqrt{a})}{2}=\frac{-4\sqrt{a}}{2}=-2\sqrt{a}\)
b)
Để \(M=-4\Leftrightarrow -2\sqrt{a}=-4\Leftrightarrow \sqrt{a}=2\Rightarrow a=4\)

bài 2 ) a) đk : \(a>0;b>0\)
b) P = \(\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2+4\sqrt{ab}}{\sqrt{a}+\sqrt{b}}.\dfrac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}\)
P = \(\dfrac{a-2\sqrt{ab}+b+4\sqrt{ab}}{\sqrt{a}+\sqrt{b}}.\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}}\)
P = \(\dfrac{a+2\sqrt{ab}+b}{\sqrt{a}+\sqrt{b}}.\sqrt{a}-\sqrt{b}\) = \(\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2}{\sqrt{a}+\sqrt{b}}.\sqrt{a}-\sqrt{b}\) = \(\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)\) = \(a-b\)
c) ta có P = \(a-b\) thay \(a=2\sqrt{3};b=\sqrt{3}\) vào ta có
P = \(2\sqrt{3}-\sqrt{3}=\sqrt{3}\) vậy khi \(a=2\sqrt{3};b=\sqrt{3}\) thì P = \(\sqrt{3}\)
bài 1) a) P = \(\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{\sqrt{a}-1}{\sqrt{a}+1}\right)\)
P = \(\dfrac{\left(a\sqrt{a}-1\right)\left(a+\sqrt{a}\right)-\left(a\sqrt{a}+1\right)\left(a-\sqrt{a}\right)}{\left(a+\sqrt{a}\right)\left(a-\sqrt{a}\right)}+\dfrac{a-1}{\sqrt{a}}.\dfrac{\left(\sqrt{a}+1\right)^2+\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
P = \(\dfrac{a^2\sqrt{a}+a^2-a-\sqrt{a}-\left(a^2\sqrt{a}-a^2+a-\sqrt{a}\right)}{\left(a+\sqrt{a}\right)\left(a-\sqrt{a}\right)}+\dfrac{a-1}{\sqrt{a}}.\dfrac{a+2\sqrt{a}+1+a-2\sqrt{a}+1}{a-1}\)
P = \(\dfrac{a^2\sqrt{a}+a^2-a-\sqrt{a}-a^2\sqrt{a}+a^2-a+\sqrt{a}}{\left(a+\sqrt{a}\right)\left(a-\sqrt{a}\right)}+\dfrac{2a+2}{\sqrt{a}}\)
P = \(\dfrac{2a^2-2a}{a^2-a}+\dfrac{2a+1}{\sqrt{a}}\) = \(\dfrac{2\left(a^2-a\right)}{a^2-a}+\dfrac{2a+2}{\sqrt{a}}\)
P = \(2+\dfrac{2a+2}{\sqrt{a}}\) = \(\dfrac{2a+2\sqrt{a}+2}{\sqrt{a}}\)
b) ta có P = 7 \(\Leftrightarrow\) \(\dfrac{2a+2\sqrt{a}+2}{\sqrt{a}}=7\) \(\Leftrightarrow\) \(2a+2\sqrt{a}+2=7\sqrt{a}\)
\(\Leftrightarrow\) \(2a-5\sqrt{a}+2=0\) (1)
đặc \(\sqrt{a}=u\) \(\left(u\ge0\right)\) (1) \(\Leftrightarrow\) \(2u^2-5u+2\)
\(\Delta=\left(-5\right)^2-4.2.2\) = \(25-16=9>0\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(u_1=\dfrac{5+3}{4}=\dfrac{8}{4}=2\left(tmđk\right)\)
\(u_2=\dfrac{5-3}{4}=\dfrac{2}{4}=\dfrac{1}{2}\left(tmđk\right)\)
ta có : \(u=\sqrt{a}=2\Leftrightarrow x=4\)
\(u=\sqrt{a}=\dfrac{1}{2}\Leftrightarrow a=\dfrac{1}{4}\)
vậy \(a=4;a=\dfrac{1}{4}\) thì P = 7

a: \(P=\sqrt{a}\left(\sqrt{a}-1\right)-2\sqrt{a}-1+2\left(\sqrt{a}+1\right)\)
\(=a-\sqrt{a}-2\sqrt{a}-1+2\sqrt{a}+2\)
\(=a-\sqrt{a}+1\)
b: \(P=\left(\sqrt{a}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\)
Dấu '=' xảy ra khi a=1/4

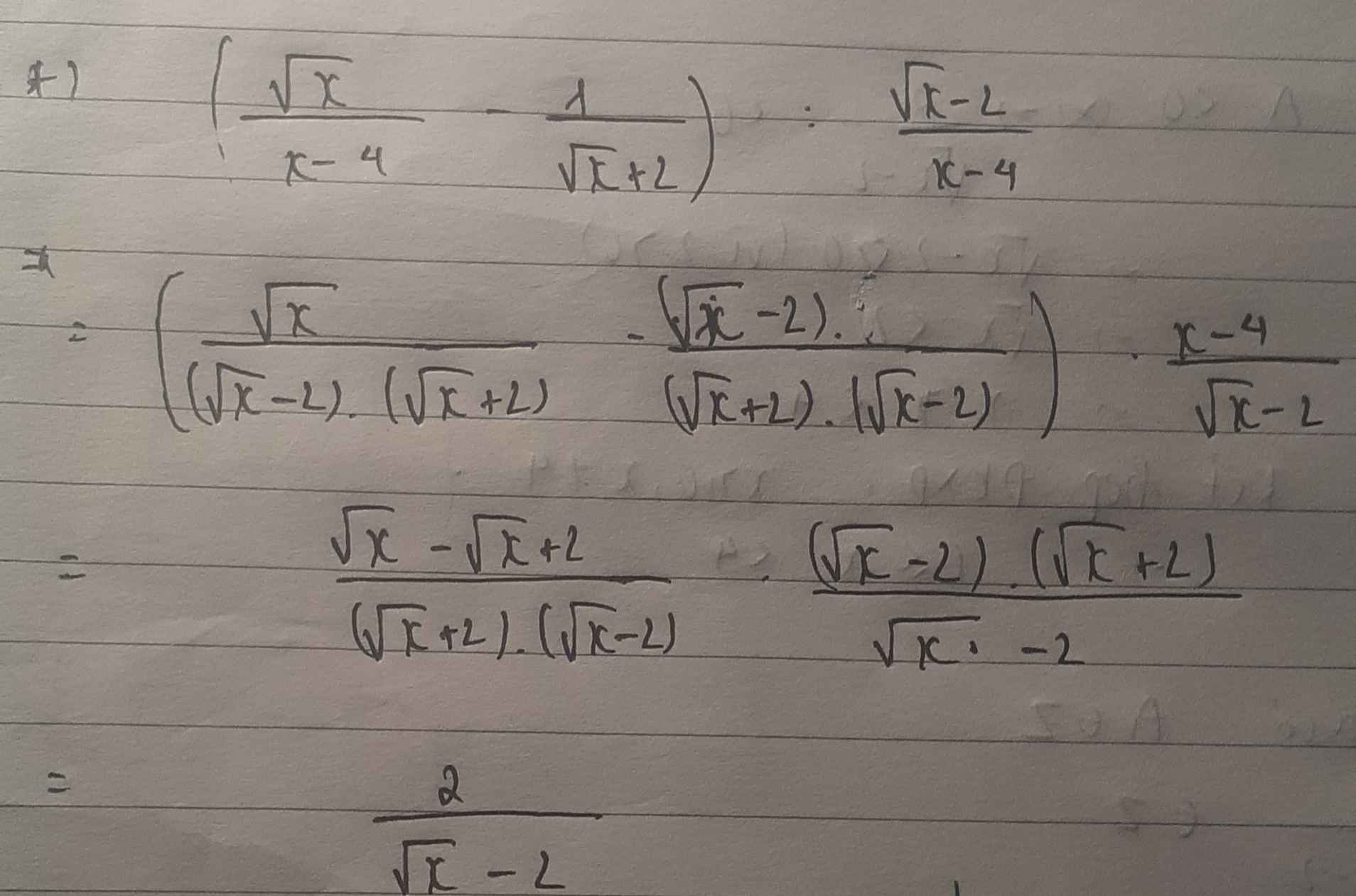


\(1.ĐKXĐ\left\{{}\begin{matrix}a>0\\a\ne1\end{matrix}\right.\)
\(M=\frac{a+1}{\sqrt{a}}+\frac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\frac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(\Leftrightarrow M=\frac{a+1}{\sqrt{a}}+\frac{a+\sqrt{a}+1}{\sqrt{a}}-\frac{a-\sqrt{a}+1}{\sqrt{a}}\)
\(\Leftrightarrow M=\frac{a+2\sqrt{a}+1}{\sqrt{a}}\)
2.
có \(M=\frac{a+2\sqrt{a}+1}{\sqrt{a}}\)
\(\Leftrightarrow M=4+\frac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}}\)
vì \(a>0\) và \(a\ne0\)
\(\Rightarrow\frac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}}>0\Leftrightarrow4+\frac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}}>4\)
Vậy M > 4
3.
M > 4\(\Leftrightarrow0\le N< \frac{3}{2}=1,5\)
Để N nhận giá trị nguyên
\(\Rightarrow N=1\)
\(\Rightarrow\frac{6}{M}=1\Leftrightarrow M=6\)
\(\Rightarrow\frac{a+2\sqrt{a}+1}{\sqrt{a}}=6\Leftrightarrow a+2\sqrt{a}+1=6\sqrt{a}\)
\(\Leftrightarrow a-4\sqrt{a}+1=0\)
Có \(\Delta`=2+1=3>0\)
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{a}=2+\sqrt{3}\left(tm\right)\\\sqrt{a}=2-\sqrt{3}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow a=7+4\sqrt{3}\)
Vậy \(a=7+4\sqrt{3}\) thì N nhận giá trị nguyên