Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình như sai đầu bài r bn, đáng là DE song song vs BC
xét tg ABC có:
AD=DB ( gt )
AE=EC ( gt )
=> DE là đường trung bình của tg ABC
=> DE sog sog BC ( tính chất đg trung bình )
=> DE= BC: 2 ( ___________________)

a: Xét ΔABH và ΔACH có
AB=AC
BH=CH
AH chung
Do đó: ΔABH=ΔACH
=>góc BAH=góc CAH
=>AH là phân giác của góc BAC
b: Xét ΔAEH và ΔADH có
AE=AD
góc EAH=góc DAH
AH chung
Do đo; ΔAEH=ΔADH
=>góc AEH=góc ADH=90 độ
=>HE vuông góc với AB
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

Giải
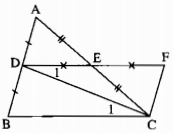
a) Xét ∆ADE và ∆CFE, ta có:
AE = CE (gt)
ˆAED = CEF^ (đối đỉnh)
DE = FE(gt)
Suy ra: ∆ADE = ∆CFE (c.g.c)
⇒⇒ AD = CF (hai cạnh tương ứng)
Mà AD = DB (gt)
Vậy: DB = CF
b) Ta có: ∆ADE = ∆CFE (chứng minh trên)
⇒ˆADE = CFE^ (2 góc tương ứng)
⇒⇒ AD // CF (vì có cặp góc so le trong bằng nhau)
Hay AB // CF
Xét ∆DBC = ∆CDF, ta có:
BD = CF (chứng minh trên)
ˆBDC = ˆFCD (hai góc so le trong vì CF // AB)
DC cạnh chung
Suy ra: ∆BDC = ∆FCD(c. g. c)
c) Ta có: ∆BDC = ∆FCD (chứng minh trên)
Suy ra: ˆC1 = ˆD1 (hai góc tương ứng)
Suy ra: DE // BC (vì có hai góc so le trong bằng nhau)
\(\Delta\)BDC = ∆FCD => BC = DF (hai cạnh tương ứng)
Mà DE = 1 : 2 . DF(gt). Vậy DE = 1 : 2 . BC
a/Xét ΔAED va ΔCEF có:
AE=CE(vì E là trung điểm của AC)
∠AED=∠CEF(đối đỉnh)
ED=EF(vì E là trung điểm của DF)
nên: ΔAED=ΔCEF(c-g-c)
do đó: AD=CF
mà AD=BD (vì D là trung điểm của AB)
vậy BD=CF
b/Ta có: ∠EAD=∠ECF(vì ΔAED=ΔCEF)
mà hai góc này ở vị trí so le trong
nên AB//CF
Ta có:AB//CF(cmt)
nên ∠BDC=∠FCD (hai góc so le trong)
Xét: ΔBDC và ΔFCD có:
DC là cạnh chung
∠BDC=∠FCD(cmt)\
DB=CF(cmt)
nên ΔBDC=ΔFCD(c-g-)
c/Ta có: ∠BCD=∠FDC(vì ΔBDC=ΔFCD)
mà hai góc này ở vị trí so le trong
nên DE//BC
Ta có: \(DE=\dfrac{1}{2}DF\)(vì E là trung điểm của DF)
mà DF=CB(vì ΔFCD=ΔBDC)
vậy \(DE=\dfrac{1}{2}CB\)
A B C F E D

Xét 2 tam giác AIE và tam giác DCE ta có: EI=ED(gt);AE=EC(vì E là trung điem của AC); góc AEI=góc DEC(vì 2 góc đoi đinh)=>tam giác AIE=tam giác DCE(c.g.c)=>AI=DC(2 cạnh tương ứng)

Xét tam giác AED và tam giác CEF có:
AE = CE (E là trung điểm của AC)
AED = CEF (2 góc đối đỉnh)
ED = EF (E là trung điểm của DF)
=> Tam giác AED = Tam giác CEF (c.g.c)
=> AD = CF (2 cạnh tương ứng) mà AD = DB (D là trung điểm của AB) => DB = CF
ADE = CFE (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => AD // CF
Xét tam giác BDC và tam giác FCD có:
BD = FC (chứng minh trên)
BDC = FCD (2 góc so le trong, AD // CF)
CD chung
=> Tam giác BDC = Tam giác FCD (c.g.c)
=> BCD = FDC (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => DE // BC
BC = FD (2 cạnh tương ứng) mà DE = 1/2 FD (E là trung điểm của FD) => DE = 1/2 BC
Xét tam giác AED và tam giác CEF có:
AE = CE (E là trung điểm của AC)
AED = CEF (2 góc đối đỉnh)
ED = EF (E là trung điểm của DF)
=> Tam giác AED = Tam giác CEF (c.g.c)
=> AD = CF (2 cạnh tương ứng) mà AD = DB (D là trung điểm của AB) => DB = CF
ADE = CFE (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => AD // CF
Xét tam giác BDC và tam giác FCD có:
BD = FC (chứng minh trên)
BDC = FCD (2 góc so le trong, AD // CF)
CD chung
=> Tam giác BDC = Tam giác FCD (c.g.c)
=> BCD = FDC (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => DE // BC
BC = FD (2 cạnh tương ứng) mà DE = 1/2 FD (E là trung điểm của FD) => DE = 1/2 BC

Rất Sorry bạn nha.Mik mới nghĩ ra câu a,b thôi,còn câu c thì mik cần thời gian:(

Bạn tự chứng minh bổ đề đường trung bình nha.
a.
Do N là trung điểm của DE;I là trung điểm của BE nên NI là đường trung bình của tam giác BDE nên:
\(IN=\frac{1}{2}BD\left(1\right)\)
Mặt khác:M là trung điểm của BC,I là trung điểm của BE nên MI là đường trung bình của tam giác BEC nên:
\(IM=\frac{1}{2}EC\left(2\right)\)
Mà \(BD=EC\) nên từ (1);(2) suy ra \(IN=MI\Rightarrow\Delta IMN\) cân tại I.
b.
Do IN là đường trung bình nên \(IN//AB\Rightarrow\widehat{APQ}=\widehat{INM}\left(3\right)\)
Do IM là đường trung bình nên \(IM//EC\Rightarrow\widehat{AQP}=\widehat{IMN}\left(4\right)\)
Từ (3);(4) suy ra \(\widehat{APQ}=\widehat{AQP}\Rightarrow\Delta APQ\) cân tại A.
F A B C D E
Trên tia đối của ED lấy F sao cho DE = FE
+) Xét ΔEAD và ΔECF có :
EA = EC ( E là trung điểm của AC )
\(\widehat{AED}=\widehat{FEC}\) ( đối đỉnh )
ED = EF ( gt )
=> ΔEAD = ΔECF ( c.g.c )
\(\Rightarrow\widehat{EAD}=\widehat{ECF}\) ( 2 góc tương ứng ) ; mà 2 góc ở vị trí so le trong
=> AB // CF => \(\widehat{BDC}=\widehat{FCD}\) ( 2 góc so le trong )
+) AD = CF ( ΔEAD = ΔECF )
mà AD = BD ( D là trung điểm AB )
=> CF = BD
+) Xét ΔBDC và FCD có :
BD = FC ( cmt )
\(\widehat{BDC}=\widehat{FCD}\left(cmt\right)\)
DC là cạnh chung
=> ΔBDC = ΔFCD ( c.g.c )
\(\widehat{BCD}=\widehat{FDC}\) ( 2 góc tương ứng )
mà 2 góc ở vị trí so le trong => DE // BC
+) Ta có : ED = EF ( gt ) => E là trung điểm DF
=> \(DE=\dfrac{1}{2}DF=\dfrac{DF}{2}\)
mà DF = BC ( ΔBDC = ΔFCD )
\(\Rightarrow DE=\dfrac{BC}{2}\)