Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta ABC\) có:
c) Ta có \(\Delta ABC\) cân tại \(A\left(cmt\right).\)
=> \(\widehat{B}=\widehat{C}\) (tính chất tam giác cân).
Xét 2 \(\Delta\) vuông \(HBM\) và \(KCM\) có:
\(\widehat{MHB}=\widehat{MKC}=90^0\left(gt\right)\)
\(BM=CM\) (như ở trên)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
=> \(\Delta HBM=\Delta KCM\) (cạnh huyền - góc nhọn).
=> \(HM=KM\) (2 cạnh tương ứng).
Chúc bạn học tốt!

(tự vẽ hình )
câu 4:
a) có AB2 + AC2 = 225
BC2 = 225
Pytago đảo => \(\Delta ABC\)vuông tại A
b) Xét \(\Delta MAB\)và \(\Delta MDC\)
MA = MD (gt)
BM = BC ( do M là trung điểm của BC )
\(\widehat{AMB}=\widehat{CMD}\)( hai góc đối đỉnh )
=> \(\Delta MAB\)= \(\Delta MDC\) (cgc)
c) vì \(\Delta MAB\)= \(\Delta MDC\)
=> \(\hept{\begin{cases}AB=DC\\\widehat{MAB}=\widehat{MDC}\end{cases}}\)
=> AB// DC
lại có AB \(\perp\)AC => DC \(\perp\)AC => \(\Delta KCD\)vuông tại C
Xét \(\Delta\) vuông ABK và \(\Delta\)vuông KCD:
AB =CD (cmt)
AK = KC ( do k là trung điểm của AC )
=> \(\Delta\)vuông AKB = \(\Delta\)vuông CKD (cc)
=> KB = KD
d. do KB = KD => \(\Delta KBD\)cân tại K
=> \(\widehat{KBD}=\widehat{KDB}\)(1)
có \(\Delta ADC\)vuông tại C => \(AD=\sqrt{AC^2+DC^2}=15\)
=> MD = 7.5
mà MB = 7.5
=> MB = MD
=> \(\Delta MBD\)cân tại M
=> \(\widehat{MBD}=\widehat{MDB}\)(2)
Từ (1) và (2) => \(\widehat{KBD}-\widehat{MBD}=\widehat{KDB}-\widehat{MDB}\)hay \(\widehat{KBM}=\widehat{KDM}\)
Xét \(\Delta KBI\)và \(\Delta KDN\)có:
\(\widehat{KBI}=\widehat{KDN}\)(cmt)
\(\widehat{KBD}\)chung
KD =KB (cmt)
=> \(\Delta KBI\)= \(\Delta KDN\)(gcg)
=> KN =KI
=. đpcm
câu 5:
a) Xét \(\Delta ABM\)và \(\Delta MDC\):
MA=MD(gt)
MB=MC (M là trung điểm của BC)
\(\widehat{BMA}=\widehat{DMC}\)( đối đỉnh )
=> \(\Delta BMA=\Delta CMD\)(cgc)
b) Xét \(\Delta\)vuông ABC
có AM là đường trung tuyến của tam giác
=> \(AM=\frac{1}{2}BC\)mà \(BM=MC=\frac{1}{2}BC\)(do M là trung điểm của BC )
=> AM = BM = MC
có MA =MD => AM = MD =MB =MC
=> BM +MC = AM +MD hay BC =AD
Xét \(\Delta BAC\)và \(\Delta DCA\)
AB =DC
AC chung
BC =DC
=> \(\Delta BAC\)= \(\Delta DCA\)(ccc)
c. Xét \(\Delta ABM\)
BM=AM
\(\widehat{ABM}\)= 600
=> đpcm

a b c m d 1 2 3 4 e f
Xét T/G ABC và DCM
CÓ ; M1=M2 ( đối đỉnh) CM=BM (M là trung điểm BC) AM=MD (gt) -> ABC=DCM(CgC)
Có T/G ABC=DCM -> Góc D=BAM(2 góc tương ứng )mà 2 góc Sole trong -> AB//DC
C) Xét T/G BFM và CEM có CM=MB(GT) E3=F4=90 độ M4=M3 ( đối đỉnh) -> BFM=CEM(g.c.g)
-> ME=MF -> M là trung điểm EF
A B C M D E F
a, Xét t/g ABM và t/g DCM có:
AM=DM(gt)
BM=CM(gt)
góc AMB=góc DMC (đối đỉnh)
=>t/g ABM=t/g DCM (c.g.c)
b, Vì t/g ABM=t/g DCM (cmt) => góc ABM = góc DCM (2 góc t/ứ)
Mà 2 góc này là cặp góc so le trong
=> AB//DC
c, Xét t/g BEM và t/g CFM có:
góc BEM = góc CFM = 90 độ (gt)
BM=CN(gt)
góc BME = góc CMF (đối đỉnh)
=>t/g BEM = t/g CFM (cạnh huyền - góc nhọn)
=>EM=FM (2 cạnh t/ứ)
=>M là trung điểm của EF

a) Xét ΔABM và ΔECM có
BM=CM(AM là trung tuyến)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
AM=EM(gt)
Do đó: ΔABM=ΔECM(c-g-c)
b) Ta có: ΔABM=ΔECM(cmt)
⇒AB=EC(hai cạnh tương ứng)(1)
Xét ΔBHA vuông tại H và ΔBHF vuông tại H có
HA=HF(gt)
BH chung
Do đó: ΔBHA=ΔBHF(hai cạnh góc vuông)
⇒AB=FB(hai cạnh tương ứng)(2)
Từ (1) và (2) suy ra BF=CE(đpcm)
c) Ta có: ΔABM=ΔECM(cmt)
⇒\(\widehat{ABM}=\widehat{ECM}\)(hai góc tương ứng)
hay \(\widehat{ABC}=\widehat{ECM}\)(3)
Xét ΔABC có AB<AC(gt)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
nên \(\widehat{ACB}< \widehat{ABC}\)(định lí quan hệ giữa cạnh và góc đối diện trong tam giác)
hay \(\widehat{ACM}< \widehat{ABC}\)(4)
Từ (3) và (4) suy ra \(\widehat{ACM}< \widehat{ECM}\)(đpcm)

a: Xét ΔABM và ΔDCM có
MA=MD
góc AMB=góc DMC
MB=MC
Do đó: ΔABM=ΔDCM
b: ΔABM=ΔDCM
nên góc ABM=góc DCM
=>AB//DC
c: ΔABC cân tại A
mà MA là trung tuyến
nên AM vuông góc với BC

a) Vì M là trung điểm của BC
=> BM = CM
Xét tam giác ABM và tam giác DCM có:
AM = DM(gt)
góc AMB = DMC (đối đỉnh)
VM = CM (cmt)
=> đpcm
b) Xét tam giác BDM và tam giác CMA có:
BM = CM (cmt)
góc BMD = CMA (đối đỉnh)
DM = AM (gt)
=> tam giác BDM = tam giác CMA (cgc)
=> BD = AC( 2 cạnh tương ứng)
góc ACM = góc DBM (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong của 2 đường thẳng BD và AC
=> BD//AC

Hình thì chú tự vẽ nhá
d) Xét tam giác AEF có AE = AF ( chứng minh phần c ) nên tam giác AEF cân tại A
Nên \(\widehat{AEF}=\widehat{AFE}=\frac{180^o-\widehat{EAF}}{2}\)
Xét \(\Delta BNE\)và \(\Delta CIF\)có :
\(\widehat{BNE}=\widehat{CIF}=90^o;BE=CF;\widehat{AEF}=\widehat{AFE}\)
Khi đó \(\Delta BNE=\Delta CIF\)( cạnh huyền góc nhọn )
Nên \(NE=IF\)(hai cạnh tương ứng )
Ta có \(AN+NE=AE;AI+IF=AF\)mà \(AE=AF;NE=IF\)nên \(AN=AI\)
Xét tam giác ANI có AN = AI nên tam giác ANI cân tại A nên \(\widehat{ANI}=\widehat{AIN}=\frac{180^o-\widehat{NAI}}{2}\)
Khi đó \(\widehat{ANI}=\widehat{AEF}=\frac{180^o-\widehat{EAF}}{2}\)mà hai góc này nằm ở vị trí đồng vị của NI và EF cắt bởi AE nên theo dấu hiệu nhận biết hai đường thẳng song song ta có \(NI//EF\)
Vậy....
A E F B C M N I
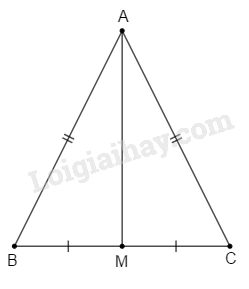
a) Xét ha tam giác ABM và ACM có:
\(\hept{\begin{cases}BM=MC\left(gt\right)\\AM:chung\\AB=AC\left(gt\right)\end{cases}\Rightarrow\Delta ABM=\Delta ACM\left(c-c-c\right)}\)
b) Ta có: AB = AC => tam giác ABC cân tại A
Tam giác cân ABC có AM là đường trung tuyến
Nên cũng đồng thời là đường cao
Suy ra: AM vuông góc với BC
c) Ta có: Tam giác ABC cân tại A => \(\widehat{ABM}=\widehat{ACM}\)
Mà \(\widehat{ABM}+\widehat{ABE}=180^0\)
\(\widehat{ACM}+\widehat{ACF}=180^0\)
Suy ra: \(\widehat{ABE}=\widehat{ACF}\)
Xét hai tam giác ABE và ACF có:
\(\hept{\begin{cases}BE=CF\\\widehat{ABE}=\widehat{ACF}\\AB=AC\end{cases}\Rightarrow\Delta ABE}=\Delta ACF\left(c-g-c\right)\)
d) Ta có: AE = AF (cmt)
=> Tam giác AEF cân tại A
Suy ra: \(\widehat{AFE}=\widehat{AEF}=\frac{180^0-\widehat{EAF}}{2}\) (1)
Xét hai tam giác vuông BNE và CIF: \(\hept{\begin{cases}BE=CF\\\widehat{E}=\widehat{F}\end{cases}\Rightarrow\Delta BNE=\Delta CIF}\) (cạnh huyền -góc nhọn)
=> NE = IF
Ta có: AE = AF (Gt); NE = IF (cmt)
=> AE - NE = AF - IF
=> AN = AI
=> Tam giác ANI cân tại I
Suy ra: \(\widehat{ANI}=\widehat{AIN}=\frac{180^0-\widehat{EAF}}{2}\) (2)
Từ (1) và (2) suy ra: \(\widehat{AIN}=\widehat{AFE}\)
Mà hai góc này ở vị trí đồng vị
Nên NI // EF

a) Xét tgiac ABM và tgiac ACM có:
AB = AC (gt)
góc ABM = góc ACM (gt)
MB = MC (gt)
suy ra: tgiac ABM = tgiac ACM (c.g.c)
b) tgiac ABM = tgiac ACM
=> góc AMB = góc AMC
mà góc AMB + góc AMC = 1800
=> góc AMB = góc AMC = 900
hay AM vuông góc với BC
c) Xét tgiac MBK và tgiac MCA có
MB = MC (gt)
góc BMK = góc CMA (dd)
MK = MA (gt)
suy ra: tgiac MBK = tgiac MCA (c.g.c)
=> góc MBK = góc MCA
mà 2 góc này so le trong
=> BK // MC
A B C M K
CM : Xét tam giác ABM và tam giác ACM
có AB = AC (gt)
BM = CM (gt)
AM : chung
=> tam giác ABM = tam giác ACM (c.c.c)
b) Ta có : Tam giác ABM = tam giác ACM (cmt)
=> góc BMA = góc AMC (hai góc tương ứng)
Mà góc BMA + góc AMC = 1800 ( kề bù )
hay 2\(\widehat{BMA}\)= 1800
=> góc BMA = 1800 : 2
=> góc BMA = 900
c) Xét tam giác AMK và tam giác CMA
có MK = MA (gt)
góc BMK = góc AMC ( đối đỉnh)
BM = CM (gt)
=> tam giác AMK = tam giác CMA (c.g.c)
=> góc KBM = góc MCA (hai góc tương ứng)
Mà góc KBM và góc MCA ở vị trí so le trong
=> Bk // AC