Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời................
Tớ không biết đúng hay sai đâu nha Ý Phạm
a,Xét tam giác ABE (BAE^ vuông) và tam giác HBE (BHE^ vuông) có:
BE=BE (cạnh chung)
ABE^=HBE^
⟹ ABE^=HBE^(ch+gn)
b,Ta có:
BA=BH (tam giác ABE = tam giác HBE)
EA=EH (________________________)
⟹ BE là đường trung trực của AH
c,Xét tam giác EKA và tam giác ECH có
AE=EH (gt)
EAK^=EHK^(=90o)
AEK^=HEC^(đối đỉnh)
⟹Tam giác EKA=tam giacsEHK (g-c-g)
⟹EK=EH ( cạnh tương ứng)
d,Từ điểm E đến đường thẳng HC có:
EH là đường vuông góc
EC là đường xiên
⟹EH<EC( quan hệ đường vuông góc)
Mà EH=AE(tam giác ABE = tam giác HBE)
⟹AE<AC

a)Xét ΔABE và ΔHBE, ta có
:
( BE là đường phân giác BE).
BE là cạnh chung.
=> ΔABE = ΔHBE
b)
BA =BH và EA = EH (ΔABE = ΔHBE)
=> BE là đường trung trực của AH .
c)
Xét ΔKAE và ΔCHE, ta có :
(gt)
EA = EH (cmt)
( đối đỉnh).
=> ΔKAE =ΔCHE
=> EK = EC(hai cạnh tuong ứng)
d)
Xét ΔKAE vuông tại A, ta có :
KE > AE (KE là cạnh huyền)
Mà : EK = EC (cmt)
=> EC > AC.

đề ngay chỗ K là giao điểm của AB và HE là sao mk vẽ ko được???
8789

a) xét tam giác ABE và tam giác HBE có
BE chung
góc ABE = góc EBH( BE là tia phân giác )
góc BAE = góc BCE
=> tam giác ABE = tam giác HBE
b) theo câu a) ta có: tam giác ABE = tam giác HBE
=> góc BEA = góc BEH (1)
mặt khác góc AEK = góc HEC (2)
cộng từng vế của (1) và (2) => góc BEK = góc BEC
xét tam giác BEK và tam giác BEC có:
BE chung
góc BEK=góc BEC ( đã c/m)
góc KBE = góc CBE ( BE là tia phân giác )
=> tam giác BEK = tam giác BEC
=>EK=EC

B A c E h k
a) áp dụng định lý Pitago tính được BC=10
b) Xét 2 tam giác có BAE = BHE = 90 , ABE = HBE vì BE là phân giác , BE chung => 2 tam giác bằng nhau theo ch-gn
c)Xét tam giác AKE và HCE có EAK = EHC = 90, AE=HE , AEH = HEC vì đối đỉnh => EK = EC
AE= HE
Xét tam giác EHC vuông tại h có EC là canh huyền => EC dài hơn HE
Từ 2 điều trên => AE<EC


A B C E H K
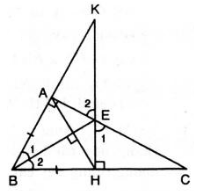
a) Xét t/giác ABE và t/giác HBE
có góc A = góc BHE = 900 (gt)
BE : chung
góc ABE = góc EBH (gt)
=> t/giác ABE = t/giác HBE (ch - gn)
b) Do t/giác ABE = t/giác HBE (cmt)
=> EA = EH (hai cạnh tương ứng)
Ta có: góc BAE + góc EAK = 1800 (gt)
=> góc EAK = 1800 - góc BAE = 1800 - 900 = 900
Xét t/giác AEK và t/giác HEC
có góc EAK = góc EHC (cmt)
AE = EH (cmt)
góc AEK = góc HEC (đối đỉnh)
=> t/giác AEK = t/giác HEC (g.c.g)
=> EK = EC (hai cạnh tương ứng)
c) Ta có : t/giác ABE = t/giác HBE (cm câu a)
=> AB = HB (hai cạnh tương ứng)
Ta lại có: t/giác AEK = t/giác HEC (cm câu b)
=> góc K = góc C (hai góc tương ứng)
Xét t/giác BKH và t/giác BCA
có góc K = góc C (cmt)
BH =AB (cmt)
góc B : chung
=> t/giác BKH = t/giác BCA (g.c.g)
=> BC = KH (hai cạnh tương ứng)