Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BFED có
ED//BF
FE//BD
Do đó: BFED là hình bình hành
Xét ΔABC có
D là trung điểm của BC
DE//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
EF//CB
Do đó: F là trung điểm của AB
Xét ΔCDE và ΔEFA có
CD=EF
DE=FA
CE=EA
Do đó: ΔCDE=ΔEFA
b: Gọi ΔABC có F là trung điểm của AB,E là trung điểm của AC
Trên tia FE lấy điểm E sao cho E là trung điểm của FK
Xét tứ giác AFCK có
E là trung điểm của AC
E là trung điểm của FK
Do đó: AFCK là hình bình hành
Suy ra: AF//KC và KC=AF
hay KC//FB và KC=FB
Xét tứ giác BFKC có
KC//FB
KC=FB
Do đó: BFKC là hình bình hành
Suy ra: FE//BC(ĐPCM)

Cho tam giác ABC có trực tâm H , trọng tâm G , O là tâm đường tròn
ngoại tiếp , I là trung điểm BC , AD là đường kính của (O) .
Chứng minh H , G , O thẳng hàng ?
Giải :
Ta có : góc DCA = góc DBA = 90 độ ( góc nội tiếp chắn 1/2 (O))
Xét tứ giác BHCD ta có :
BH // DC ( vì cùng vuông góc với AC )
CH // DB ( vì cùng vuông góc với AB )
Do đó tứ giác BHCD là hình bình hành .
===> H , I , D thẳng hàng và IH = ID (t/c đường chéo hbhành)
Ta lại có : OI = 1/2 AH ( đ.trung bình tam giác DAH ) (1)
GI = 1/2 GA (t/chất trọng tâm của ABC ) (2)
góc HAG = góc GIO ( so le trong vì AH // OI ) (3)
Do đó tam giác GAH đồng dạng tam giác GIO ( c.g.c)
===> góc HGA = góc IGO (góc tương ứng của 2 t.giác đ.dạng )
Vì góc HGA và góc IGO là 2 góc ở vị trí đối đỉnh bằng nhau nên ta suy ra H , G , O thẳng hàng .
Vậy trong 1 tam giác trực tâm , trọng tâm , tâm đường tròn ngoại tiếp cùng nằm trên 1 đường thẳng đó là đường thẳng Euler !

a) Tứ giác ANHM có 3 góc vuông : AMH ; MAN ; ANH nên là hình chữ nhật
b) Hình chữ nhật ANHM có AH cắt MN tại trung điểm mỗi đường nên OA =\(\frac{AH}{2};ON=\frac{MN}{2}\)mà AH = MN nên OA = ON
\(\Rightarrow\Delta OAN\)cân tại O (1)
Ta lại có :\(\Delta ABC,\Delta AHC\)lần lượt vuông tại A,H có\(\widehat{B}+\widehat{C}=\widehat{HAC}+\widehat{C}=90^0\Rightarrow\widehat{B}=\widehat{OAN}=\widehat{ONA}\)(do 1)
mà\(\widehat{ONA}+\widehat{ONC}=180^0\)(kề bù).Vậy tứ giác BCNM có\(\widehat{B}+\widehat{MNC}=180^0\Rightarrow\widehat{C}+\widehat{BMN}=180^0\)
c)\(\Delta ANM,\Delta ABC\)cùng vuông tại A có\(\widehat{B}=\widehat{MNA}\Rightarrow\Delta ANM~\Delta ABC\left(g-g\right)\Rightarrow\frac{AN}{AM}=\frac{AB}{AC}\)=> AM.AB = AN.AC
d)\(\Delta ABC\)vuông tại A có I là trung điểm BC nên trung tuyến AI =\(\frac{BC}{2}\)mà BI =\(\frac{BC}{2}\)nên AI = BI
\(\Rightarrow\Delta ABI\)cân tại I =>\(\widehat{BAI}=\widehat{B}=\widehat{MNA}\)mà\(\Delta AMN\)vuông tại A có\(\widehat{AMN}+\widehat{MNA}=90^0\)
Gọi giao điểm AI và MN là P thì\(\Delta AMP\)có \(\widehat{MAP}+\widehat{AMP}=90^0\)nên\(\Delta AMP\)vuông tại P => AI _|_ MN

Gọi D, E, F theo thứ tự là trung điểm của BC, CA, AB. Đường trung trực của BC phải vuông góc với EF (vì (EF // BC), hay nó là một đường cao của tam giác DEF. Suy ra ba đường trung trực của tam giác ABC là ba đường cao của tam giác DEF. Do đó tâm đường tròn ngoại tiếp tam giác ABC (giao điểm của ba đường trung trực của tam giác ABC) là trực tâm của tam giác DEF.

Bài này là chứng minh đường thẳng ơ le.
cách 1:
Gọi E,FE,F lần lượt là trung điểm của BC,AC. Ta có EF là đường trung bình của tam giác ABC nên EF//AB.
Ta lại có OF//BH(cùng vuông góc với ACA). Do đó : ˆOFE=ˆABH
Tương tự ˆOEF=ˆBAH
Từ đó ta có tam giác ABH đồng dạng với tam giác EFO
Suy ra AH/OE=AB/EF=2
mà AG/GE=2.
Do đó: AG/EG=AH/OE=2
mà ˆHAG=ˆOEG
⇒ΔHAG∼ΔEOG⇒ˆHGA=ˆEGO
nên ˆHGA+ˆAGO=ˆHGO=180
Vậy H,G,O thẳng hàng.
C2 : dùng véc tơ để tính
C3: dựng đường tròn 9 điểm => ...
Ta có : góc DCA = góc DBA = 90 độ ( góc nội tiếp chắn \(\frac{1}{2}\) (O))
Xét tứ giác \(BHCD,\) ta có : \(BH\) // \(DC\) ( vì cùng vuông góc với \(AC\))
\(CH\)// \(DB\) ( vì cùng vuông góc với AB )
Do đó tứ giác \(BHCD\) là hình bình hành .
\(\Rightarrow\) \(H,\)\(I,\)\(D\) thẳng hàng và \(IH=ID\) (tính chất đường chéo hình bình hành)
Ta lại có : \(OI=\frac{1}{2}AH\) ( đường trung bình tam giác \(DAH\) ) \(\left(1\right)\)
\(GI=\frac{1}{2}GA\) (tính chất trọng tâm của \(ABC\) ) \(\left(2\right)\)
Góc\(HAG\) = góc \(GIO\) ( so le trong vì \(AH\) // \(OI\) ) \(\left(3\right)\)
Do đó tam giác \(GAH\) đồng dạng tam giác \(GIO\) ( c.g.c)
\(\Rightarrow\) góc \(HGA\) = góc \(IGO\) (góc tương ứng của 2 tam giác đồng dạng )
Vì góc \(HGA\) và góc \(IGO\) là 2 góc ở vị trí đối đỉnh bằng nhau nên ta suy ra \(H,\) \(G,\)\(O,\)thẳng hàng .
Vậy trong 1 tam giác trực tâm, trọng tâm, tâm đường tròn ngoại tiếp cùng nằm trên 1 đường thẳng đó là đường thẳng Euler !

) Gọi M là trung điểm BC. Lấy điểm D sao cho O là trung điểm CD
Xét Δ BCD có M là trung điểm BC, O là trung điểm CD OM là đường trung bình của Δ BCD
OM=12DB và OM // DB
mà OM⊥BC ( OM là đường trung trực của BC ) DB⊥BC
mà AH⊥BC( AH là đường cao của ΔABC ) AH // DB
Xét ΔABH và ΔBAD có
HABˆ=DBAˆ( 2 góc so le trong do AH // DB )
AB chung
ABHˆ=BADˆ( 2 góc so le trong do AH // DB )
ΔABH=ΔBAD( g-c-g )
AH = BD mà OM=12DB OM=12AH
AH = 2 OM ( đpcm )
b) Gọi G' là giao điển của AM và OH, P là trung điểm G'H, Q là trung điểm G'A
Xét Δ AG'H có P là trung điểm G'H, Q là trung điểm G'A PQ là đường trung bình của \large\Delta AG'H
PQ=12AH và PQ // AH
Do PQ=12AH mà OM=12AH PQ = OM
Do AH // OM ( cùng ⊥BC ) mà PQ // AH PQ // OM
Xét ΔPQG′ và ΔOMG′ có
PQG′ˆ=OMG′ˆ( 2 góc so le trong do PQ // OM)
PQ = OM (c/m trên )
QPG′ˆ=MOG′ˆ ( 2 góc so le trong do PQ //OM )
ΔPQG′=ΔOMG′( g-c-g )
G'Q = G'M và G'P = G'O
Ta có G'Q = G'M mà G′Q=12G′A( Q là trung điểm G'A ) G′M=12G′Amà G'M + G'A = AM
G′A=23AM mà AM là trung tuyến của ΔABC
G' là trọng tâm của ΔABC ,mà G là trọng tâm của ΔABC G′≡ G
mà G′∈OH G∈OH O, H, G thẳng hàng ( đpcm )
Hên xui nghe bạn ^ ^

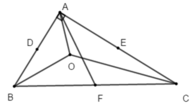
+ Vì O là giao điểm của ba đường phân giác trong tam giác ABC nên O là tâm của đường tròn nội tiếp tam giác ABC nên đáp án A sai.
+ Tam giác ABC vuông tại A có F là trung điểm của BC nên AF là đường trung tuyến ứng với cạnh huyền
Do đó: AF = 1 2 BC (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Suy ra AF = FC = FB
Nên F cách đều ba đỉnh A, B, C
Do đó F là tâm đường tròn ngoại tiếp tam giác ABC.
+ Vì D ≠ E ≠ F và chỉ có một đường tròn ngoại tiếp tam giác ABC nên đáp án B, C sai và D đúng.
Chọn đáp án D