Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BFED có
ED//BF
FE//BD
Do đó: BFED là hình bình hành
Xét ΔABC có
D là trung điểm của BC
DE//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
EF//CB
Do đó: F là trung điểm của AB
Xét ΔCDE và ΔEFA có
CD=EF
DE=FA
CE=EA
Do đó: ΔCDE=ΔEFA
b: Gọi ΔABC có F là trung điểm của AB,E là trung điểm của AC
Trên tia FE lấy điểm E sao cho E là trung điểm của FK
Xét tứ giác AFCK có
E là trung điểm của AC
E là trung điểm của FK
Do đó: AFCK là hình bình hành
Suy ra: AF//KC và KC=AF
hay KC//FB và KC=FB
Xét tứ giác BFKC có
KC//FB
KC=FB
Do đó: BFKC là hình bình hành
Suy ra: FE//BC(ĐPCM)

A B C D E F
* Xét tam giác BDE và tam giác EFB có:
+) \widehat{DEB} = \widehat{EBF} ( so le trong)
+) BE chung
+) \widehat{FEB} = \widehat{DBE} ( so le trong)
=> Tam giác BDE = tam giác EFB ( g.c.g )
=> EF = BD ( 2 cạnh tương ứng)
* Mà AD = BD ( D là trung điểm của AB)
=> EF = AD. ( cpcm)

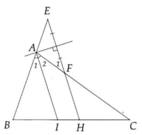

d A B C E F
kẻ BE và CF vuông góc với d thẳng d
Do ( d ) // với BC => BEFC là hình chữ nhật
\(\Rightarrow C_{ABC_{nn}}\Leftrightarrow C\left(BEA+CFE\right)_{LN}\)
\(C\left(BEA+CFA\right)_{LN}\Leftrightarrow AB=AC\)
\(\Leftrightarrow\Delta ABC\)cân