Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B C A M H D E
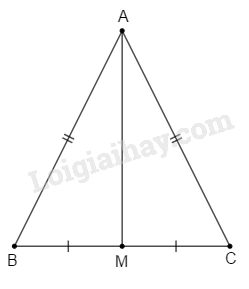
a) Xét tam giác ABM và ACM có:
AB = AC (gt)
BM = CM (gt)
Cạnh AM chung
\(\Rightarrow\Delta ABM=\Delta ACM\left(c-c-c\right)\)
b) Ta thấy tam giác MCD có HC là đường cao đồng thời trung tuyến nên ACD là tam giác cân tại C.
Vậy thì CH hay Ca là phân giác góc \(\widehat{MCD}\)
c) Xét tam giác AMC và ADC có:
CM = CD
AC chung
\(\widehat{MCA}=\widehat{DCA}\)
\(\Rightarrow\Delta AMC=\Delta ADC\left(c-g-c\right)\)
\(\Rightarrow\widehat{ADC}=\widehat{AMC}=90^o\) hay \(AD\perp CD\)
Lại có HE // AD nên \(HE\perp CD\)

Câu hỏi của Cả cuộc đời này tôi sẽ mãi yêu một người - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

c. Theo câu a, tam giác ABM= tam giác ACM (ccc) => AMB=AMC
Mà AMB+AMC=180*(kề bù)
=> AMB=90*
Xét tam giác HCM và tam giác HCD
MH=DH
MHC=DHC=90*
HC chung
=> tam giác HCM= tam giác HCD (cgc)
=> MC=CD
Theo câu b, AC là phân giác MCD
=> MCA=DCA
Xét tam giác MAC và tam giác DAC có
MC=CD
MCA=DCA
AC chung
=> tam giác MAC = tam giác DAC(cgc)
=> AMC=ADC=90*
=> AD vg CD mà HE//AD => HE vg CD
Em tham khảo tại đây nhé.
Câu hỏi của Cả cuộc đời này tôi sẽ mãi yêu một người - Toán lớp 7 - Học toán với OnlineMath

Xét \(\Delta ABC\) có:
c) Ta có \(\Delta ABC\) cân tại \(A\left(cmt\right).\)
=> \(\widehat{B}=\widehat{C}\) (tính chất tam giác cân).
Xét 2 \(\Delta\) vuông \(HBM\) và \(KCM\) có:
\(\widehat{MHB}=\widehat{MKC}=90^0\left(gt\right)\)
\(BM=CM\) (như ở trên)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
=> \(\Delta HBM=\Delta KCM\) (cạnh huyền - góc nhọn).
=> \(HM=KM\) (2 cạnh tương ứng).
Chúc bạn học tốt!

a) Xét 2 \(\Delta\) \(AMD\) và \(CMB\) có:
\(AM=CM\) (vì M là trung điểm của \(AC\))
\(\widehat{AMD}=\widehat{CMB}\) (vì 2 góc đối đỉnh)
\(MD=MB\left(gt\right)\)
=> \(\Delta AMD=\Delta CMB\left(c-g-c\right)\)
=> \(AD=BC\) (2 cạnh tương ứng).
b) Xét 2 \(\Delta\) \(BMA\) và \(DMC\) có:
\(BM=DM\left(gt\right)\)
\(\widehat{BMA}=\widehat{DMC}\) (vì 2 góc đối đỉnh)
\(MA=MC\) (vì M là trung điểm của \(AC\))
=> \(\Delta BMA=\Delta DMC\left(c-g-c\right)\)
=> \(\widehat{BAM}=\widehat{DCM}\) (2 góc tương ứng).
Mà \(\widehat{BAM}=90^0\left(gt\right)\)
=> \(\widehat{DCM}=90^0.\)
=> \(CD\perp MC\)
Hay \(CD\perp AC.\)
c) Theo câu b) ta có \(\Delta BMA=\Delta DMC.\)
=> \(\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng).
Mà 2 góc này nằm ở vị trí so le trong.
=> \(AB\) // \(CD\)
Hay \(AB\) // \(CN.\)
Có:
\(BN\) // \(AC\left(gt\right)\)
\(AB\) // \(CN\left(cmt\right)\)
=> \(AB=CN\) (tính chất đoạn chắn).
Xét 2 \(\Delta\) vuông \(ABM\) và \(CNM\) có:
\(\widehat{BAM}=\widehat{NCM}=90^0\)
\(AB=CN\left(cmt\right)\)
\(AM=CM\) (như ở trên)
=> \(\Delta ABM=\Delta CNM\) (2 cạnh góc vuông tương ứng bằng nhau) (đpcm).
Chúc bạn học tốt!

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

Em tham khảo tại đây nhé.
Câu hỏi của Cả cuộc đời này tôi sẽ mãi yêu một người - Toán lớp 7 - Học toán với OnlineMath

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔCMD có
CH là đường cao
CH là đường trung tuyến
Do đo;ΔCMD cân tại C
mà CA là đườg cao
nên CA là phân giác của góc MCD