Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\overrightarrow{MD}+\overrightarrow{MA}\)
Dựng hình bình hành AMDG \(\Rightarrow\overrightarrow{MD}+\overrightarrow{MA}=\overrightarrow{MG}\)
\(\Rightarrow MG//BC\)
Mà \(AG//MD\Rightarrow AG\perp BC\Rightarrow G\in AH\) với AH là đường cao ứng với BC
\(\Rightarrow HDMG\) là hình chữ nhật \(\Rightarrow\widehat{DGM}=\widehat{HMG}\)
Mà \(\widehat{DGM}=\widehat{GMA}\) (so le trong) \(\Rightarrow\widehat{HMG}=\widehat{GMA}\)
\(\Rightarrow\) Trong tam giác AMH, GM vừa là đường cao vừa là phân giác
\(\Rightarrow AMH\) cân tại M
Hay M nằm trên trung trực của AH
Vậy tập hợp M là trung trực của AH (hay là đường trung bình song song cạnh huyền của tam giác ABC)
b.
Vẫn dựng hình bình hành AMDG như câu a
Và do \(AG//MD\) nên ta cũng có \(AG\perp BC\) hay G nằm trên đường cao AH
\(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\overrightarrow{MD}+\overrightarrow{MA}=\overrightarrow{MG}\Rightarrow\left|\overrightarrow{MG}\right|=\left|\overrightarrow{MA}\right|\)
\(\Rightarrow\Delta AMG\) cân tại M
Gọi I là trung điểm AG \(\Rightarrow MI\perp AG\Rightarrow MIHD\) là hcn
\(\Rightarrow IH=MD\Rightarrow IH=AG=2IA\Rightarrow IA=\frac{1}{3}AH\)
\(\Rightarrow\) Tập hợp M là đường thẳng vuông góc AH và đi qua điểm I cố định nằm trên AH sao cho \(IA=\frac{1}{3}AH\)
a/ \(VT=\overrightarrow{AB}+\overrightarrow{BF}+\overrightarrow{BC}+\overrightarrow{CG}+\overrightarrow{CD}+\overrightarrow{DH}+\overrightarrow{DA}+\overrightarrow{AE}\)
\(=\left(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}\right)+\left(\frac{1}{2}\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CD}+\frac{1}{2}\overrightarrow{DA}+\frac{1}{2}\overrightarrow{AB}\right)\)
\(=\overrightarrow{0}+\frac{1}{2}.\overrightarrow{0}=\overrightarrow{0}=VP\)
b/ Câu này áp dụng luôn kq câu a
\(\overrightarrow{MF}-\overrightarrow{MA}+\overrightarrow{MG}-\overrightarrow{MB}+\overrightarrow{MH}-\overrightarrow{MC}+\overrightarrow{ME}-\overrightarrow{MD}=\overrightarrow{0}\)
chuyển mấy cái vecto kia sang vế phải là có ngay đpcm câu b
c/\(VT=\overrightarrow{AI}+\overrightarrow{IB}+\overrightarrow{AI}+\overrightarrow{IC}+\overrightarrow{AI}+\overrightarrow{ID}=3\overrightarrow{AI}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\)
Để ý tới G là TĐ CD, F là TĐ BC
Theo quy tắc trung điểm
\(\Rightarrow\overrightarrow{IB}+\overrightarrow{IC}=2\overrightarrow{IF}=2\overrightarrow{HI}\)
\(\Rightarrow\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=2\overrightarrow{HI}+\overrightarrow{ID}=\overrightarrow{HI}+\overrightarrow{HD}\)
Mà \(\overrightarrow{HD}=\overrightarrow{AH}\Rightarrow\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{HI}+\overrightarrow{AH}=\overrightarrow{AI}\)
Thay vào cái trên sẽ có đpcm
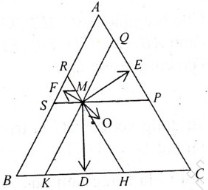
Qua M kẻ các đường thẳng song song với các cạnh của tam giác
A1B1 // AB; A2C2 // AC; B2C1 // BC.
Dễ thấy các tam giác MB1C2; MA1C1;MA2B2 đều là các tam giác đều. Ta lại có MD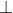 
B1C2 nên MD cũng là trung điểm thuộc cạnh B1C2 của tam giác MB1C2
Ta có 2
= 
+ 
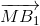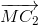
Tương tự: 2
= 
+ 
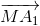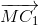
2
= 
+
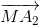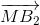
=> 2( ++) = (+) + ( + ) + (+)
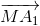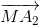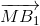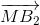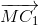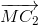Tứ giác là hình bình hành nên
+ = 
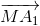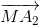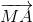
Tương tự: + =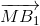 
+ = 
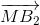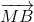
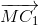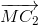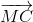
=> 2( ++) = ++
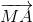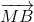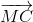
vì O là trọng tâm bất kì của tam giác và M là một điểm bất kì nên
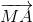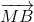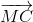++ = 3
.
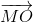Cuối cùng ta có:
2( ++) = 3;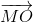
=> ++ = 
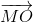
Lời giải:
\(\overrightarrow{MA}.\overrightarrow{BC}+\overrightarrow{MB}.\overrightarrow{CA}+\overrightarrow{MC}.\overrightarrow{AB}=(\overrightarrow{MB}+\overrightarrow{BA})\overrightarrow{BC}+\overrightarrow{MB}.\overrightarrow{CA}+\overrightarrow{MC}.\overrightarrow{AB}\)
\(=\overrightarrow{MB}(\overrightarrow{BC}+\overrightarrow{CA})+\overrightarrow{BA}.\overrightarrow{BC}-\overrightarrow{MC}.\overrightarrow{BA}\)
\(=\overrightarrow{MB}.\overrightarrow{BA}+\overrightarrow{BA}.\overrightarrow{BC}-\overrightarrow{MC}.\overrightarrow{BA}\)
\(=\overrightarrow{BA}(\overrightarrow{MB}+\overrightarrow{BC}-\overrightarrow{MC})=\overrightarrow{BA}(\overrightarrow{MC}-\overrightarrow{MC})=\overrightarrow{BA}.\overrightarrow{0}=0\)
Ta có đpcm.