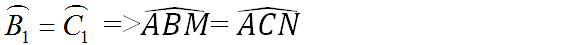K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

9 tháng 8 2020
1
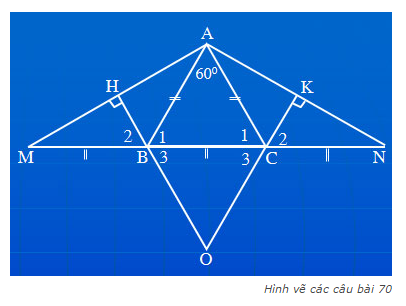
a) trước tiên chứng minh\(\widehat{ABM}=\widehat{ACN}\)
rồi mới chứng minh 2 tam giác ABM và ACN bằng nhau
suy ra AM = AN
b)Đầu tiên chứng minh\(\widehat{ABH}=\widehat{ACK}\)
rồi chứng minh hai tam giác ABH và ACK bằng nhau
suy ra BH = CK
c) vì hai tam giác ABH và ACK bằng nhau (cmt)
nên AH = AK
d) ta có \(\widehat{AMB}=\widehat{ACN}\)(hai tam giác ABH và ACK bằng nhau)
nên dễ cm \(\widehat{MBH}=\widehat{NCK}\)
còn lại tự cm
e) dễ cm tam giác ABC đều
vẽ \(BH\perp AC\)
nên BH vừa là đường cao; phân giác và trung tuyến
dễ cm \(\Delta BHC=\Delta NKC\)
nên \(\widehat{BCH}=\widehat{NCK}=60^0\)
từ đó dễ cm AMN cân và OBC dều