Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu a)
Từ \(\tan a=3\Leftrightarrow \frac{\sin a}{\cos a}=3\Rightarrow \sin a=3\cos a\)
Do đó:
\(\frac{\sin a\cos a+\cos ^2a}{2\sin ^2a-\cos ^2a}=\frac{3\cos a\cos a+\cos ^2a}{2(3\cos a)^2-\cos ^2a}\)
\(=\frac{\cos ^2a(3+1)}{\cos ^2a(18-1)}=\frac{4}{17}\)
Câu b)
Có: \(\cot \left(\frac{\pi}{2}-x\right)=\tan x=\frac{\sin x}{\cos x}\)
\(\cos\left(\frac{\pi}{2}+x\right)=-\sin x\)
\(\Rightarrow \cot \left(\frac{\pi}{2}-x\right)\cos \left(\frac{\pi}{2}+x\right)=\frac{-\sin ^2x}{\cos x}\)
Và:
\(\frac{\sin (\pi-x)\cot x}{1-\sin ^2x}=\frac{\sin x\cot x}{\cos^2x}=\frac{\sin x.\frac{\cos x}{\sin x}}{\cos^2x}=\frac{1}{\cos x}\)
Do đó:
\(\Rightarrow \cot \left(\frac{\pi}{2}-x\right)\cos \left(\frac{\pi}{2}+x\right)+\frac{\sin (\pi-x)\cot x}{1-\sin ^2x}=\frac{1-\sin ^2x}{\cos x}=\frac{\cos ^2x}{\cos x}=\cos x\)
Ta có đpcm.

a)
\(\sin ^4a-\cos ^4a+1=(\sin ^2a-\cos ^2a)(\sin ^2a+\cos^2a)+1\)
\(=(\sin ^2a-\cos ^2a).1+1=\sin ^2a-\cos ^2a+\sin ^2a+\cos ^2a\)
\(=2\sin ^2a\)
b) \(\sin ^2a+2\cos ^2a-1=(\sin ^2a+\cos^2a)+\cos ^2a-1\)
\(=1+\cos ^2a-1=\cos ^2a\)
\(\Rightarrow \frac{\sin ^2a+2\cos ^2a-1}{\cot ^2a}=\frac{\cos ^2a}{\cot ^2a}=\frac{\cos ^2a}{\frac{\cos ^2a}{\sin ^2a}}=\sin ^2a\)
c)
\(\frac{1-\sin ^2a\cos ^2a}{\cos ^2a}-\cos ^2a=\frac{1}{\cos ^2a}-\sin ^2a-\cos ^2a\)
\(=\frac{1}{\cos ^2a}-(\sin ^2a+\cos ^2a)=\frac{1}{\cos ^2a}-1\)
\(=\frac{1-\cos ^2a}{\cos ^2a}=\frac{\sin ^2a}{\cos ^2a}=\tan ^2a\)
d)
\(\frac{\sin ^2a-\tan ^2a}{\cos ^2a-\cot ^2a}=\frac{\sin ^2a-\frac{\sin ^2a}{\cos ^2a}}{\cos ^2a-\frac{\cos ^2a}{\sin ^2a}}\) \(=\frac{\sin ^2a(1-\frac{1}{\cos ^2a})}{\cos ^2a(1-\frac{1}{\sin ^2a})}\)
\(=\frac{\sin ^2a.\frac{\cos ^2a-1}{\cos ^2a}}{\cos ^2a.\frac{\sin ^2a-1}{\sin ^2a}}\) \(=\frac{\sin ^2a.\frac{-\sin ^2a}{\cos ^2a}}{\cos ^2a.\frac{-\cos ^2a}{\sin ^2a}}=\frac{\sin ^6a}{\cos ^6a}=\tan ^6a\)
f)
\(\frac{(\sin a+\cos a)^2-1}{\cot a-\sin a\cos a}=\frac{\sin ^2a+\cos ^2a+2\sin a\cos a-1}{\frac{\cos a}{\sin a}-\sin a\cos a}\)
\(=\sin a.\frac{1+2\sin a\cos a-1}{\cos a-\cos a\sin ^2a}\)
\(=\sin a. \frac{2\sin a\cos a}{\cos a(1-\sin ^2a)}=\sin a. \frac{2\sin a\cos a}{\cos a. \cos^2 a}=\frac{2\sin ^2a}{\cos ^2a}=2\tan ^2a\)

a/ \(\dfrac{\sin x+\cos x-1}{1-\cos x}=\dfrac{2\cos x}{\sin x-\cos x+1}\)
\(\Leftrightarrow-2\cos^2x+2\cos x-2\cos x+2\cos^2x=0\)
\(\Leftrightarrow0=0\) (đúng)
\(\RightarrowĐPCM\)
b/ \(\tan a.\tan b=\dfrac{\tan a+\tan b}{\cot a+\cot b}\)
\(\Leftrightarrow\tan a.\tan b.\left(\cot a+\cot b\right)=\tan a+\tan b\)
\(\Leftrightarrow\tan a.\tan b.\cot a+\tan a.\tan b.\cot b=\tan a+\tan b\)
\(\Leftrightarrow\tan b+\tan a=\tan a+\tan b\) (đúng)
\(\RightarrowĐPCM\)

Bài 1:
a)
\(\sin ^2x+\sin ^2x\cot^2x=\sin ^2x(1+\cot^2x)=\sin ^2x(1+\frac{\cos ^2x}{\sin ^2x})\)
\(=\sin ^2x.\frac{\sin ^2x+\cos^2x}{\sin ^2x}=\sin ^2x+\cos^2x=1\)
b)
\((1-\tan ^2x)\cot^2x+1-\cot^2x\)
\(=\cot^2x(1-\tan^2x-1)+1=\cot^2x(-\tan ^2x)+1=-(\tan x\cot x)^2+1\)
\(=-1^2+1=0\)
c)
\(\sin ^2x\tan x+\cos^2x\cot x+2\sin x\cos x=\sin ^2x.\frac{\sin x}{\cos x}+\cos ^2x.\frac{\cos x}{\sin x}+2\sin x\cos x\)
\(=\frac{\sin ^3x}{\cos x}+\frac{\cos ^3x}{\sin x}+2\sin x\cos x=\frac{\sin ^4x+\cos ^4x+2\sin ^2x\cos ^2x}{\sin x\cos x}=\frac{(\sin ^2x+\cos ^2x)^2}{\sin x\cos x}=\frac{1}{\sin x\cos x}\)
\(=\frac{1}{\frac{\sin 2x}{2}}=\frac{2}{\sin 2x}\)
Bài 2:
Áp dụng BĐT Cauchy Schwarz ta có:
\(P=\frac{a^2}{\sqrt{a(2c+a+b)}}+\frac{b^2}{\sqrt{b(2a+b+c)}}+\frac{c^2}{\sqrt{c(2b+c+a)}}\)
\(\geq \frac{(a+b+c)^2}{\sqrt{a(2c+a+b)}+\sqrt{b(2a+b+c)}+\sqrt{c(2b+c+a)}}(*)\)
Tiếp tục áp dụng BĐT Cauchy-Schwarz:
\((\sqrt{a(2c+a+b)}+\sqrt{b(2a+b+c)}+\sqrt{c(2b+c+a)})^2\leq (a+b+c)(2c+a+b+2a+b+c+2b+c+a)\)
\(\Leftrightarrow (\sqrt{a(2c+a+b)}+\sqrt{b(2a+b+c)}+\sqrt{c(2b+c+a)})^2\leq 4(a+b+c)^2\)
\(\Rightarrow \sqrt{a(2c+a+b)}+\sqrt{b(2a+b+c)}+\sqrt{c(2b+c+a)}\leq 2(a+b+c)(**)\)
Từ \((*); (**)\Rightarrow P\geq \frac{(a+b+c)^2}{2(a+b+c)}=\frac{a+b+c}{2}=\frac{3}{2}\)
Vậy \(P_{\min}=\frac{3}{2}\)
Dấu "=" xảy ra khi $a=b=c=1$

Lời giải:
Ta có:
\(P=\frac{2\sin \alpha+3\cos \alpha}{4\sin \alpha-5\cos \alpha}=\frac{2+\frac{3\cos \alpha}{\sin \alpha}}{4-\frac{5\cos \alpha}{\sin \alpha}}\)
\(=\frac{2+3\cot \alpha}{4-5\cot\alpha}=\frac{2+3.3}{4-5.3}=-1\)

phần chứng minh biểu thức không phụ thuộc \(x\)
ta có : \(A=\dfrac{cot^2a-cos^2a}{cot^2a}+\dfrac{sinacosa}{cota}=\dfrac{cot^2a-cos^2a}{cot^2a}+\dfrac{cos^2a}{cot^2a}\)
\(=\dfrac{cot^2a-cos^2a+cos^2a}{cot^2a}=\dfrac{cot^2a}{cot^2a}=1\left(đpcm\right)\)
ý còn lại : xem lại đề nha bn
phần chứng minh đẳng thức
ta có : \(\dfrac{sin2a-2sina}{sin2a+2sina}+tan^2\dfrac{a}{2}=\dfrac{2sinacosa-2sina}{2sinacosa+2sina}+tan^2\dfrac{a}{2}\)
\(=\dfrac{2sina\left(cosa-1\right)}{2sina\left(cosa+1\right)}+tan^2\dfrac{a}{2}=\dfrac{cosa-1}{cosa+1}+tan^2\dfrac{a}{2}\)
\(=\dfrac{1-2sin^2\dfrac{a}{2}-1}{2cos^2\dfrac{a}{2}-1+1}+tan^2\dfrac{a}{2}=\dfrac{-2sin^2\dfrac{a}{2}}{2cos^2\dfrac{a}{2}}+tan^2\dfrac{a}{2}\)
\(=-tan^2\dfrac{a}{2}+tan^2\dfrac{a}{2}=0\left(đpcm\right)\)
ta có : \(\dfrac{sina}{1+cosa}+\dfrac{1+cosa}{sina}=\dfrac{sin^2a+\left(1+cosa\right)^2}{sina\left(1+cosa\right)}\)
\(=\dfrac{sin^2a+cos^2a+2cosa+1}{sina\left(1+cosa\right)}=\dfrac{2cosa+2}{sina\left(cosa+1\right)}\)
\(=\dfrac{2\left(cosa+1\right)}{sina\left(cosa+1\right)}=\dfrac{2}{sina}\left(đpcm\right)\)
còn 2 câu kia để chừng nào rảnh mk giải cho nha
mk lm 2 câu còn lại nha
ta có : \(\dfrac{sin^2x}{sinx-cosx}-\dfrac{sinx+cosx}{tan^2x-1}=\dfrac{\left(1-cos^2x\right)\left(tan^2x-1\right)-\left(sin^2x-cos^2x\right)}{\left(sinx-cosx\right)\left(tan^2x-1\right)}\)
\(=\dfrac{tan^2x-sin^2x-sin^2x-sin^2x+cos^2x}{\left(sinx-cosx\right)\left(tan^2x-1\right)}=\dfrac{\dfrac{sin^4x}{cos^2x}-sin^2x-sin^2x+cos^2x}{\left(sinx-cosx\right)\left(tan^2-1\right)}\)
\(=\dfrac{tan^2x\left(sin^2x-cos^2x\right)-\left(sin^2x-cos^2x\right)}{\left(sinx-cosx\right)\left(tan^2x-1\right)}=\dfrac{\left(tan^2x-1\right)\left(sin^2x-cos^2x\right)}{\left(sinx-cosx\right)\left(tan^2x-1\right)}\)
\(=sinx+cosx\left(đpcm\right)\)
ta có : \(\dfrac{sin\left(a+b\right)sin\left(a-b\right)}{1-tan^2a.cot^2b}=\dfrac{sin\left(a+b\right)sin\left(a-b\right)}{1-\dfrac{sin^2a.cos^2b}{cos^2a.sin^2b}}\)
\(=\dfrac{sin\left(a+b\right)sin\left(a-b\right)}{\dfrac{cos^2a.sin^2b-sin^2a.cos^2b}{cos^2a.sin^2b}}=\dfrac{sin\left(a+b\right)sin\left(a-b\right).cos^2a.sin^2b}{-\left(sin^2a.cos^2b-cos^2a.sin^2b\right)}\)
\(=\dfrac{sin\left(a+b\right)sin\left(a-b\right).cos^2a.sin^2b}{-\left(\left(sina.cosb-cosa.sinb\right)\left(sina.cosb+cosa.sinb\right)\right)}\)
\(=\dfrac{sin\left(a+b\right)sin\left(a-b\right).cos^2a.sin^2b}{-sin\left(a-b\right)sin\left(a+b\right)}=-cos^2a.sin^2b\left(đpcm\right)\)
mk lm hơi tắc ! do tối rồi , mà mk lại đang ở quán nek nên không tiện làm dài . bạn thông cảm

\(A=\dfrac{3sin\alpha-cos\alpha}{sin\alpha+cos\alpha}=\dfrac{\dfrac{3sin\alpha}{cos\alpha}-1}{\dfrac{sin\alpha}{cos\alpha}-1}=\dfrac{3tan\alpha-1}{tan\alpha-1}\)\(=\dfrac{3\sqrt{2}-1}{\sqrt{2}-1}=5+2\sqrt{2}\).
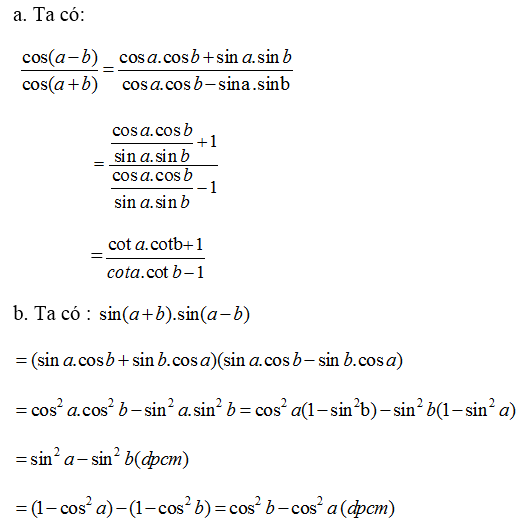
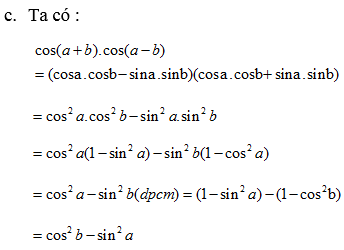
Chia tử và mẫu cho cosa ta có:
B=\(\dfrac{4\tan a+5}{2\tan a-3}\). Vì \(\cot a=\dfrac{1}{2}\) nên \(\tan a=2\)
=> B=13
chia tử và mẫu của B cho sina khác 0\(B=\dfrac{4\dfrac{sina}{sina}+5\dfrac{cosa}{sina}}{2\dfrac{sina}{sina}-3\dfrac{cosa}{sina}}=\dfrac{4+5cota}{2-3cota}=\dfrac{4+5\dfrac{1}{2}}{2-3\dfrac{1}{2}}=13\)
vay B = 13