Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
1/2 + 1/3 + 1/4 + ... + 1/15 + 1/16 = (1/2 + 1/3 + 1/4 + 1/5) + (1/6 + 1/7 + 1/8) + (1/9 + 1/10 + 1/11) + (1/12 + 1/13 + 1/14) + (1/15 + 1/16)
Vì 1/6 + 1/7 + 1/8 < 3x 1/6 = 1/2
1/9 + 1/10 + 1/11 <3x1/9 = 1/3
1/12 + 1/13 +1/14 < 3x1/12 = 1/4
1/15 + 1/16 < 3 x 1/15 = 1/5
Nên A < 2 x (1/2 + 1/3 + 1/4 + 1/5) < 2 x (1/2 + 1/2 + 1/4 + 1/4) =3 (1)
Lập luận tương tự có:
A = ( 1/2 + 1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8) + (1/9 + 1/10 + 1/11 + 1/12) + (1/13 + 1/14 + 1/15 + 1/16) > (1/2 + 1/3 + 1/4) + 4 x 1/8 + 4 x 1/ 12 + 4 x 1/16
Hay A > 2 x (1/2 + 1/3 + 1/4) > 2 x (1/2 + 1/4 + 1/4) = 2 (2)
Từ (1) và (2) ta có 2 < A < 3. Vậy A không phải là số tự nhiên.![]()

câu a ) A = 6/12 + 4/12 + 3/12
A = 6+4+3/12
A= 13/12
câub ) bạn dùng máy tính bấm hết ra
câu c ) cũng giống câu b bạn dùng máy tính bấm hết ra
![]()
![]()
![]()
OK mình đã giúp bạn xong rồi nhé !!!
mình bảo bạn bấm máy tính là vì mình lười ko bấm cho bạn thôi ***

Ta thấy A > 0 (1)
Vì \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{2016^2}< \dfrac{1}{2015.2016}\)
\(\Rightarrow A< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2015.2016}\)
\(\Rightarrow A>1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2015}-\dfrac{1}{2016}=1-\dfrac{1}{2016}=\dfrac{2015}{2016}< 1\)(2)
Từ (1)(2) => 0 < A < 1
Vậy A không phải là số tự nhiên
Giải:
Ta có: \(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{2016^2}>0_{\left(1\right)}.\) (do A là phân số dương).
Ta lại có:
\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{2016^2}.\)
\(=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2016.2016}.\)
\(< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2015.2016}.\)
\(< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2015}-\dfrac{1}{2016}.\)
\(< 1+\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3}\right)+\left(\dfrac{1}{4}-\dfrac{1}{4}\right)+...+\left(\dfrac{1}{2015}-\dfrac{1}{2015}\right)-\dfrac{1}{2016}.\)\(< 1+0+0+0+...+0-\dfrac{1}{2016}.\)
\(< 1-\dfrac{1}{2016}.\)
\(< \dfrac{2015}{2016}.\)
\(\Rightarrow A< 1_{\left(2\right)}.\) (do \(\dfrac{2015}{2016}< 1\)).
Từ \(_{\left(1\right)}\) và \(_{\left(2\right)}\) \(\Rightarrow0< A< 1.\)
\(\Rightarrow A\) không phải là số tự nhiên.
Vậy ta thu được \(đpcm.\)
~ Học tốt!!! ~

Xét 1/2 + 1/3 + 1/4
1/2 + 1/4 = (2+4)/(2.4) = 2.3/[(3-1)(3+1)] = 2.3/(3^2 - 1) > 2.3/3^2 = 2/3 = 2.(1/3)
---> 1/2+1/3+1/4 > 3.(1/3) = 1 (1)
Lại xét 1/5 + 1/6 + ... + 1/9 + ... + 1/13
1/8+1/10 = (8+10)/(8.10) = 2.9/(9^2 - 1) > 2.9/9^2 = 2/9 = 2.(1/9)
Tương tự cm được 1/7+1/11 > 2.(1/9) ; 1/6+1/12 > 2.1/9; ...; 1/5+1/13 > 2.1/9
---> 1/5+1/6+ ... + 1/13 > 9.(1/9) = 1 (2)
Tiếp tục xài chiêu đó, cm được 1/14+1/15+ ... + 1/38 > 25.(1/25) = 1 (3)
(1),(2),(3) ---> a > 3 (*)
Mặt khác
1/2 + 1/3 + 1/6 = 1 (4)
1/4 + 1/5 + 1/20 = 1/2 (5)
1/7 + 1/8 + 1/9 < 3.(1/7) = 3/7 (6)
1/10+1/11+ ...+1/14 < 5.(1/10) = 1/2 (7)
1/15+1/16+ ...+1/19 < 5.(1/15) = 1/3 (8)
1/21+1/22+ ...+1/26 < 6.(1/21) = 2/7 (9)
1/27+1/28+ ...+1/50 < 24.(1/27) = 8/9 (10)
Cộng (4),(5),(6),(7), (8),(9),(10) ---> a < 2 + 5/7 + 11/9 < 2 + 7/9 + 11/9 = 4 (**)
Từ (*) và (**) ---> 3 < a < 4 ---> a ko phải là số tự nhiên.

a)Ta có:\(\dfrac{1}{b}-\dfrac{1}{b+1}=\dfrac{b+1-b}{b\left(b+1\right)}=\dfrac{1}{b^2+b}< \dfrac{1}{b^2}\)(do b>1)
\(\dfrac{1}{b-1}-\dfrac{1}{b}=\dfrac{b-b+1}{\left(b-1\right)b}=\dfrac{1}{b^2-b}>\dfrac{1}{b^2}\)(do b>1)
b)Áp dụng từ câu a
=>\(\dfrac{1}{2}-\dfrac{1}{3}< \dfrac{1}{2^2}< \dfrac{1}{1}-\dfrac{1}{2}\)
\(\dfrac{1}{3}-\dfrac{1}{4}< \dfrac{1}{3^2}< \dfrac{1}{2}-\dfrac{1}{3}\)
.........................
\(\dfrac{1}{9}-\dfrac{1}{10}< \dfrac{1}{9^2}< \dfrac{1}{8}-\dfrac{1}{9}\)
=>\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}< S< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}\)
=>\(\dfrac{1}{2}-\dfrac{1}{10}< S< 1-\dfrac{1}{9}\)
=>\(\dfrac{2}{5}< S< \dfrac{8}{9}\)(đpcm)

Không tính thì sao mà làm được :)
a)
\(2020-\dfrac{1}{3^2}-\dfrac{1}{4^2}-...-\dfrac{1}{2019^2}\)
\(=3+\left(1-\dfrac{1}{3^2}\right)+\left(1-\dfrac{1}{4^2}\right)+....+\left(1-\dfrac{1}{2019^2}\right)\)
\(=3+\left(\dfrac{3^2-1}{3^2}+\dfrac{4^2-1}{4^2}+...+\dfrac{2019^2-1}{2019^2}\right)\)
\(=3+\left(\dfrac{2\cdot4}{3^2}+\dfrac{3\cdot5}{4^2}+\dfrac{4\cdot6}{5^2}+\dfrac{5\cdot7}{6^2}+...+\dfrac{2018\cdot2020}{2019^2}\right)\)
\(=3+\dfrac{\left(2\cdot3\cdot4\cdot....\cdot2018\right)}{3\cdot4\cdot5\cdot6...\cdot2019}\cdot\dfrac{\left(3\cdot4\cdot5\cdot....\cdot2020\right)}{3\cdot4\cdot5\cdot6\cdot....\cdot2019}=3+\dfrac{2\cdot2020}{2019}\)
\(=\dfrac{10097}{2019}\)
Có: \(\dfrac{1}{k^2}=\dfrac{1}{k.k}< \dfrac{1}{\left(k-1\right)k}\left(k\in\text{ℕ},k>0\right)\)
\(\Rightarrow A=2020-\dfrac{1}{3^2}-\dfrac{1}{4^2}-\dfrac{1}{5^2}-...-\dfrac{1}{2019^2}\)
\(A=2020-\left(\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+...+\dfrac{1}{2019^2}\right)\)
\(>2020-\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{2018.2019}\right)\)
Có: \(\dfrac{1}{k-1}-\dfrac{1}{k}=\dfrac{1}{k\left(k-1\right)}\left(k\in\text{ℕ},k>0\right)\)
\(\Rightarrow A>2020-\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-...+\dfrac{1}{2018}-\dfrac{1}{2019}\right)\)
\(A>2020-\dfrac{1}{2}+\dfrac{1}{2019}\)>2,2
Có: \(B=\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{17}\)
\(B=\dfrac{1}{5}+\left(\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}\right)\)\(< \dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{6}+...+\dfrac{1}{6}\)
\(=\dfrac{1}{5}+\dfrac{1}{6}.12=2+\dfrac{1}{5}=2,2\)
Vậy A>B.

Giải:
Các phân số thuộc tổng trên khi quy đồng mẫu chứa lũy thừa của \(2\) với số mũ lớn nhất là \(2^5.\)
\(\Rightarrow\) Khi quy đồng mẫu số, các phân số đều có tử chẵn, chỉ có phân số \(\dfrac{1}{32}\) có tử lẻ.
\(\Rightarrow\) Tổng trên có tử lẽ, mẫu chẵn, không phải là số tự nhiên.
Vậy \(A\) không phải là số tự nhiên. \((đpcm)\)
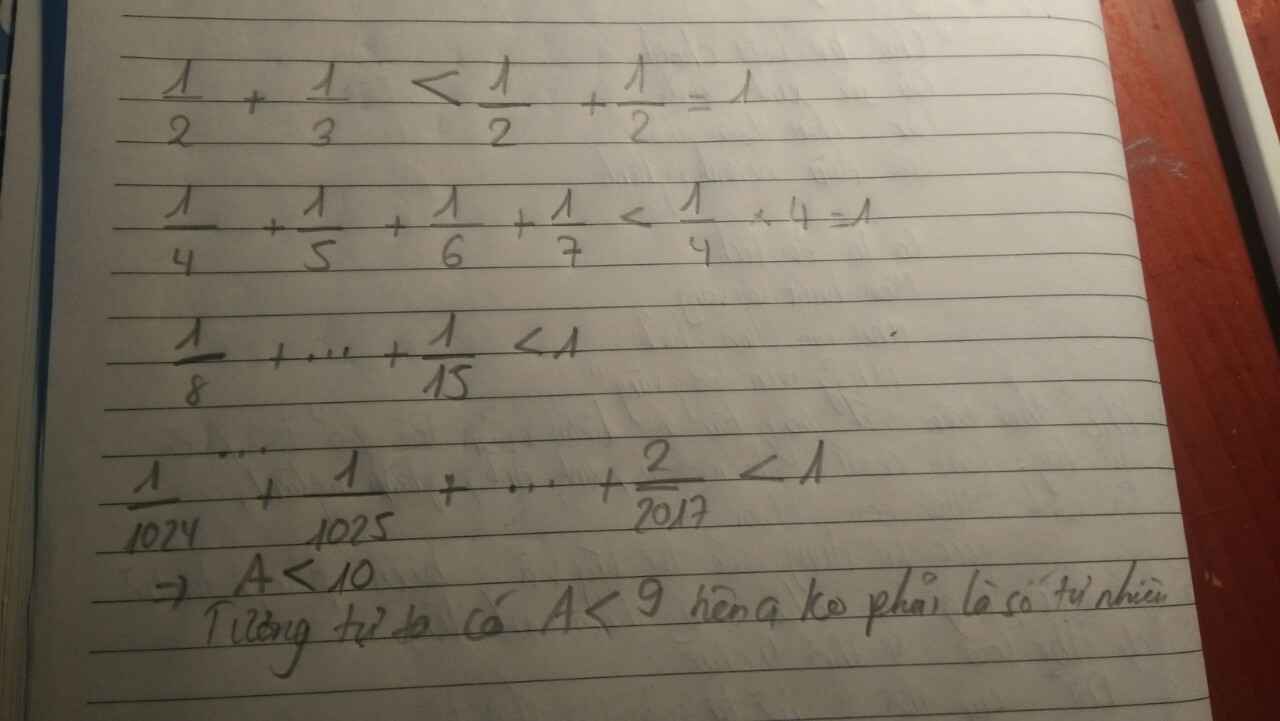
A=1/2+1/3+..+1/2019 < 1>
A= 1+1/2+1/3+..+1/2019 < 1>
A=1+1/2+1/3+..+1/2019 <1>
A=1+1/2+1/3+..+1/2019 <2018>
Vì 2018/2019 <1>
nên A=1/2+1/3+..+1/2019<1>
=> A=1/2+1/3+..+1/2019 không phải là số tự nhiên.
Mình chưa hiểu cách bạn làm với dấu <1> cho lắm.
Theo mình hiểu thì bạn đang chứng minh $A< 1$ nên $A$ không phải số tự nhiên. Mà điều này thì sai vì $A=1+(\frac{1}{2}+\frac{1}{3}+...)$ hiển nhiên lớn hơn $1$.