Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(3-m=\frac{10}{x+2}\)
\(\Leftrightarrow\left(3-m\right)\left(x+2\right)=10\)
=> 3-m và x+2 thuộc Ư (10)={1;2;5;10}
TH1: \(\hept{\begin{cases}3-m=1\\x+2=10\end{cases}\Leftrightarrow\hept{\begin{cases}m=2\\x=8\end{cases}}}\)hoặc \(\hept{\begin{cases}3-m=10\\x+2=1\end{cases}\Leftrightarrow\hept{\begin{cases}m=-7\\x=1\end{cases}}}\)
TH2: \(\hept{\begin{cases}3-m=5\\x+2=2\end{cases}\Leftrightarrow\hept{\begin{cases}m=-2\\x=0\end{cases}}}\)hoặc \(\hept{\begin{cases}3-m=2\\x+2=5\end{cases}\Leftrightarrow\hept{\begin{cases}m=1\\x=-3\end{cases}}}\)(loại)
bài 3:
\(A=\frac{2x^3-6x^2+x-8}{x-3}\left(x\ne3\right)\)
\(\Leftrightarrow A=\frac{\left(2x^3-6x^2\right)+\left(x-8\right)}{x-3}=\frac{2x\left(x-3\right)+\left(x-8\right)}{x-3}=2x+\frac{x-8}{x-3}\)
Để A nguyên thì \(\frac{x-8}{x-3}\)nguyên
Có: \(\frac{x-8}{x-3}=\frac{x-3-5}{x-3}=1-\frac{5}{x-3}\)
Vì x nguyên => x-3 nguyên => x-3 \(\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Ta có bảng
| x-3 | -5 | -1 | 1 | 5 |
| x | -2 | 2 | 4 | 8 |

a trước nhé, vì muốn P là số nguyên nên a sẽ chia hết cho a^2-a+1
=>a^2-a+1 - a^2 + a chia hết cho a ( Theo tc chia hết )
=>1 chia hết cho a
=>a thuộc Ư(1) nói cách khác, a=1

a) P xác định khi và chỉ khi \(\hept{\begin{cases}2x+3\ne0\\2x+1\ne0\end{cases}}\Rightarrow x\ne\frac{-3}{2};x\ne\frac{-1}{2}\)
b) \(P=\frac{2}{2x+3}+\frac{3}{2x+1}-\frac{6x+5}{\left(2x+3\right)\left(2x+1\right)}\)
\(\Rightarrow P=\frac{2\left(2x+1\right)+3\left(2x+3\right)-\left(6x+5\right)}{\left(2x+3\right)\left(2x+1\right)}\)
\(\Rightarrow P=\frac{4x+2+6x+9-6x-5}{\left(2x+3\right)\left(2x+1\right)}\)
\(\Rightarrow P=\frac{4x+6}{\left(2x+3\right)\left(2x+1\right)}=\frac{2\left(2x+3\right)}{\left(2x+3\right)\left(2x+1\right)}\)
\(=\frac{2}{2x+1}\)
Vậy \(P=\frac{2}{2x+1}\)
c) \(P=1\Leftrightarrow\frac{2}{2x+1}=1\Leftrightarrow2x+1=2\Leftrightarrow x=\frac{1}{2}\left(tmdkxđ\right)\)
\(P=-3\Leftrightarrow\frac{2}{2x+1}=-3\Leftrightarrow2x+1=\frac{-2}{3}\Leftrightarrow x=\frac{-5}{6}\left(tmđkđ\right)\)
Vậy \(x=\frac{1}{2}\)thì P = 1; \(x=\frac{-5}{6}\)thì P = -3
d) \(P>0\Leftrightarrow\frac{2}{2x+1}>0\Leftrightarrow2x+1>0\Leftrightarrow x>\frac{-1}{2}\)
Vậy \(x>\frac{-1}{2}\)thì P > 0

a)
Để A nguyên \(\Leftrightarrow x^3+x⋮x-1\)
\(\Leftrightarrow x^3-1+x+1⋮x-1\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)+x+1⋮x-1\left(1\right)\)
Vì x nguyên \(\Rightarrow\hept{\begin{cases}x-1\in Z\\x^2+x+1\in Z\end{cases}}\)
\(\Rightarrow\left(x-1\right)\left(x^2+x+1\right)⋮x-1\left(2\right)\)
Từ (1) và (2) \(\Rightarrow x+1⋮x-1\)
\(\Leftrightarrow x-1+2⋮x-1\)
Mà \(x-1⋮x-1\)
\(\Rightarrow2⋮x-1\)
\(\Rightarrow x-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(\Rightarrow x\in\left\{-1;0;2;3\right\}\)
Vậy \(x\in\left\{-1;0;2;3\right\}\)
b) Để B nguyên \(\Leftrightarrow x^2-4x+5⋮2x-1\)
\(\Leftrightarrow2x^2-8x+10⋮2x-1\)
\(\Leftrightarrow\left(2x^2-x\right)-\left(6x-3\right)-\left(x-7\right)⋮2x-1\)
\(\Leftrightarrow x\left(2x-1\right)-3\left(2x-1\right)-\left(x-7\right)⋮2x-1\)
\(\Leftrightarrow\left(2x-1\right)\left(x-3\right)-\left(x-7\right)⋮2x-1\left(1\right)\)
Vì x nguyên \(\Rightarrow\hept{\begin{cases}2x-1\in Z\\x-3\in Z\end{cases}}\)
\(\Rightarrow\left(2x-1\right)\left(x-3\right)⋮2x-1\left(2\right)\)
Từ (1) và(2) \(\Rightarrow x-7⋮2x-1\)
\(\Leftrightarrow2x-14⋮2x-1\)
\(\Leftrightarrow2x-1-13⋮2x-1\)
Mà \(2x-1⋮2x-1\)
\(\Rightarrow13⋮2x-1\)
\(\Rightarrow2x-1\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
Làm nốt nha các phần còn lại bạn cứ dựa bài mình mà làm

MK ko biế đúng ko nữa , sai thì ý kiến
a)
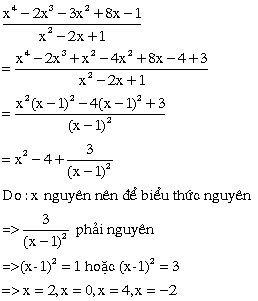
b)
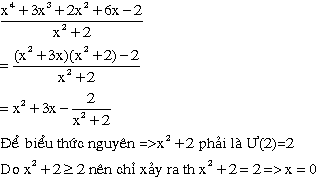
Chúc các bn hok tốt
Tham khảo nhé

a) A = \(\frac{3x^2+3x-3}{x^2+x-2}-\frac{x+1}{x+2}+\frac{x-2}{x}\cdot\left(\frac{1}{1-x}-1\right)\)
A = \(\frac{3x^2+3x-3}{x^2+2x-x-2}-\frac{x+1}{x+2}+\frac{x-2}{x}\cdot\left(\frac{1-1+x}{1-x}\right)\)
A = \(\frac{3x^2+3x-3}{\left(x-1\right)\left(x+2\right)}-\frac{x+1}{x+2}+\frac{x-2}{x}\cdot\frac{x}{1-x}\)
A = \(\frac{3x^2+3x-3}{\left(x-1\right)\left(x+2\right)}-\frac{x+1}{x+2}-\frac{x-2}{x-1}\)
A = \(\frac{3x^2+3x-3}{\left(x-1\right)\left(x+2\right)}-\frac{\left(x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x+2\right)}-\frac{\left(x-2\right)\left(x+2\right)}{\left(x-1\right)\left(x+2\right)}\)
A = \(\frac{3x^2+3x-3-x^2+1-x^2+4}{\left(x-1\right)\left(x+2\right)}\)
A = \(\frac{x^2+3x+2}{\left(x-1\right)\left(x+2\right)}\)
A = \(\frac{x^2+2x+x+2}{\left(x-1\right)\left(x+2\right)}\)
A = \(\frac{\left(x+1\right)\left(x+2\right)}{\left(x-1\right)\left(x+2\right)}\)
A = \(\frac{x+1}{x-1}\) (Đk: \(x-1\ge0\) => x \(\ge\)1)
b) Ta có: A = \(\frac{x+1}{x-1}=\frac{\left(x-1\right)+2}{x-1}=1+\frac{2}{x-1}\)
Để A \(\in\)Z <=> 2 \(⋮\)x - 1
<=> x - 1 \(\in\)Ư(2) = {1; -1; 2; -2}
<=> x \(\in\){2; 0; 3; -1}
c) Ta có: A < 0
=> \(\frac{x+1}{x-1}< 0\)
=> \(\hept{\begin{cases}x+1< 0\\x-1>0\end{cases}}\) hoặc \(\hept{\begin{cases}x+1>0\\x-1< 0\end{cases}}\)
=> \(\hept{\begin{cases}x< -1\\x>1\end{cases}}\)(loại) hoặc \(\hept{\begin{cases}x>-1\\x< 1\end{cases}}\)
=> -1 < x < 1
Edogawa Conan
Thiếu dòng đầu \(ĐKXĐ:\hept{\begin{cases}x\ne1\\x\ne-2\\x\ne0\end{cases}}\)

P=n3+4n-5=n3-n+5n-5=n(n2-1)+5(n-1)
=n(n-1)(n+1)+5(n-1)=(n-1)[n(n+1)+5]
=(n-1)(n2+n+5)
Vì n \(\in\) N nên n2+n+5 > 1
Để P là số nguyên tố thì n-1=1=>n=2
Thử lại thấy n=2 thỏa mãn
Vậy n=2

BÀI 1:
a) \(ĐKXĐ:\) \(x-3\)\(\ne\)\(0\)
\(\Leftrightarrow\)\(x\)\(\ne\)\(3\)
b) \(A=\frac{x^3-3x^2+4x-1}{x-3}\)
\(=\frac{\left(x^3-3x^2\right)+\left(4x-12\right)+11}{x-3}\)
\(=\frac{x^2\left(x-3\right)+4\left(x-3\right)+11}{x-3}\)
\(=x^2+4+\frac{11}{x-3}\)
Để \(A\)có giá trị nguyên thì \(\frac{11}{x-3}\)có giá trị nguyên
hay \(x-3\)\(\notinƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
Ta lập bảng sau
\(x-3\) \(-11\) \(-1\) \(1\) \(11\)
\(x\) \(-8\) \(2\) \(4\) \(14\)
Vậy....
2)\(A=\frac{6x-5}{3x+1}=\frac{6x+2-7}{3x+1}=\frac{2\left(3x+1\right)-7}{3x+1}=2-\frac{7}{3x+1}\)
Do đó, để A nhận giá trị nguyên thì 7 chia hết cho 3x+1 hay (3x+1)EƯ(7)={1;-1;7;-7}
=>3xE{0;-2;6;-8}
=>xE{0;2}
*)Nếu x=0 thì A=2-\(\frac{7}{3\cdot0+1}=2-7=-5\)
*)Nếu x=2 thì A=2-\(\frac{7}{3\cdot2+1}=2-1=1\)
=>Để A có GTNN thì x=0
Vậy để A nhận giá trị nguyên thì xE{0;2}
Để A có GTNN là -5 thì x=0