Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ \(\Delta'=4-m+1=5-m\)
Để pt có 2 nghiệm pb đều dương <=> \(\left\{{}\begin{matrix}5-m>0\\x_1+x_2>0\\x_1.x_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 5\\4>0\left(lđ\right)\\m-1>0\end{matrix}\right.\Leftrightarrow1< m< 5\)
b/ \(x_1^3+x_2^3=40\Leftrightarrow\left(x_1+x_2\right)\left(x_1^2-x_1x_2+x_2^2\right)=40\)
\(\Leftrightarrow\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-3x_1x_2\right]=40\)
\(\Leftrightarrow4\left(4^2-3\left(m-1\right)\right)=40\Leftrightarrow64-12m+12=40\)
\(\Leftrightarrow m=3\)
2/ Ko hiểu ý của câu này ntn :)

a: TH1: m=1
Pt sẽ là -(2*1-1)x+1+1=0
=>-x+2=0
=>x=2(loại)
TH2: m<>1
\(\text{Δ}=\left(2m-1\right)^2-4\left(m-1\right)\left(m+1\right)\)
\(=4m^2-4m+1-4m^2+4=-4m+5\)
Để phương trình có hai nghiệm phân biệt thì -4m+5>0
=>m<5/4
Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}x_1-3x_2=0\\x_1+x_2=\dfrac{2m-1}{m-1}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x_2=\dfrac{-2m+1}{m-1}\\x_1=3x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{2m-1}{4\left(m-1\right)}\\x_1=\dfrac{6m-3}{4m-4}\end{matrix}\right.\)
x1x2=m+1/m-1
=>\(\dfrac{\left(2m-1\right)\left(6m-3\right)}{16\left(m-1\right)^2}=\dfrac{m+1}{m-1}\)
=>\(\dfrac{\left(2m-1\right)\left(6m-3\right)}{16\left(m-1\right)^2}=\dfrac{16\left(m-1\right)\left(m+1\right)}{16\left(m-1\right)^2}\)
=>\(16m^2-16=12m^2-12m+3\)
=>4m^2+12m-19=0
hay \(x=\dfrac{-3\pm2\sqrt{7}}{2}\)
c: \(\text{Δ}=\left(2m-2\right)^2-12\left(3m-5\right)\)
\(=4m^2-8m+4-36m+60=4m^2-44m+64\)
Để phương trình có hai nghiệm phân biệt thì m^2-11m+16>0
=>\(\left\{{}\begin{matrix}x< \dfrac{11-\sqrt{57}}{2}\\x>\dfrac{11+\sqrt{57}}{2}\end{matrix}\right.\)
Theo đề, ta có hệ:
x1-x2=0 và x1+x2=2m-2/3
=>2x1=(2m-2)/3 và x1=x2
=>x1=x2=m-1/3
x1*x2=3m-5/3
=>\(\dfrac{m^2-2m+1}{9}=\dfrac{3m-5}{3}\)
=>m^2-2m+1=9m-15
=>m^2-11m+16=0
hay \(m\in\varnothing\)


1.
Đặt \(x^2-2x+m=t\), phương trình trở thành \(t^2-2t+m=x\)
Ta có hệ \(\left\{{}\begin{matrix}x^2-2x+m=t\\t^2-2t+m=x\end{matrix}\right.\)
\(\Rightarrow\left(x-t\right)\left(x+t-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=t\\x=1-t\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=x^2-2x+m\\x=1-x^2+2x-m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-x^2+3x\\m=-x^2+x+1\end{matrix}\right.\)
Phương trình hoành độ giao điểm của \(y=-x^2+x+1\) và \(y=-x^2+3x\):
\(-x^2+x+1=-x^2+3x\)
\(\Leftrightarrow x=\dfrac{1}{2}\Rightarrow y=\dfrac{5}{4}\)
Đồ thị hàm số \(y=-x^2+3x\) và \(y=-x^2+x+1\):
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi \(m< \dfrac{5}{4}\)
Mà \(m\in\left[-10;10\right]\Rightarrow m\in[-10;\dfrac{5}{4})\)
Có cách nào lm bài này bằng cách lập bảng biến thiên k ạ

\(x^3-x^2+2mx-2m=0\)
\(\Leftrightarrow x^2\left(x-1\right)+2m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2=-2m\end{matrix}\right.\)
Để pt có 3 nghiệm \(\Rightarrow-2m>0\Rightarrow m< 0\)
a. Do vai trò 3 nghiệm như nhau, ko mất tính tổng quát giả sử \(x_1=1\) và \(x_2;x_3\) là nghiệm của \(x^2+2m=0\)
Để pt có 3 nghiệm pb \(\Rightarrow\left\{{}\begin{matrix}-2m>0\\-2m\ne1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< 0\\m\ne-\dfrac{1}{2}\end{matrix}\right.\)
Khi đó: \(x_2+x_3=0\Rightarrow x_1+x_2+x_3=1\ne10\) với mọi m
\(\Rightarrow\) Không tồn tại m thỏa mãn yêu cầu
b.
Giả sử pt có 3 nghiệm, khi đó \(\left[{}\begin{matrix}x_2=-\sqrt{-2m}< 0< 1\\x_3=\sqrt{-2m}\end{matrix}\right.\)
\(\Rightarrow\) Luôn có 1 nghiệm của pt âm \(\Rightarrow\) không tồn tại m thỏa mãn
Em coi lại đề bài

Phương trình có 2 nghiệm khi \(\Delta'=m^2-4\ge0\Rightarrow\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=4\end{matrix}\right.\)
\(\left(\dfrac{x_1}{x_2}\right)^2+\left(\dfrac{x_2}{x_1}\right)^2=3\)
\(\Rightarrow\left(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}\right)^2-2=3\)
\(\Rightarrow\left(\dfrac{x_1^2+x_2^2}{x_1x_2}\right)^2=5\)
\(\Rightarrow\left(\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{4}\right)^2=5\)
\(\Rightarrow\left(m^2-2\right)^2=5\)
\(\Rightarrow m^2=2+\sqrt{5}\)
\(\Rightarrow m=\pm\sqrt{2+\sqrt{5}}\)


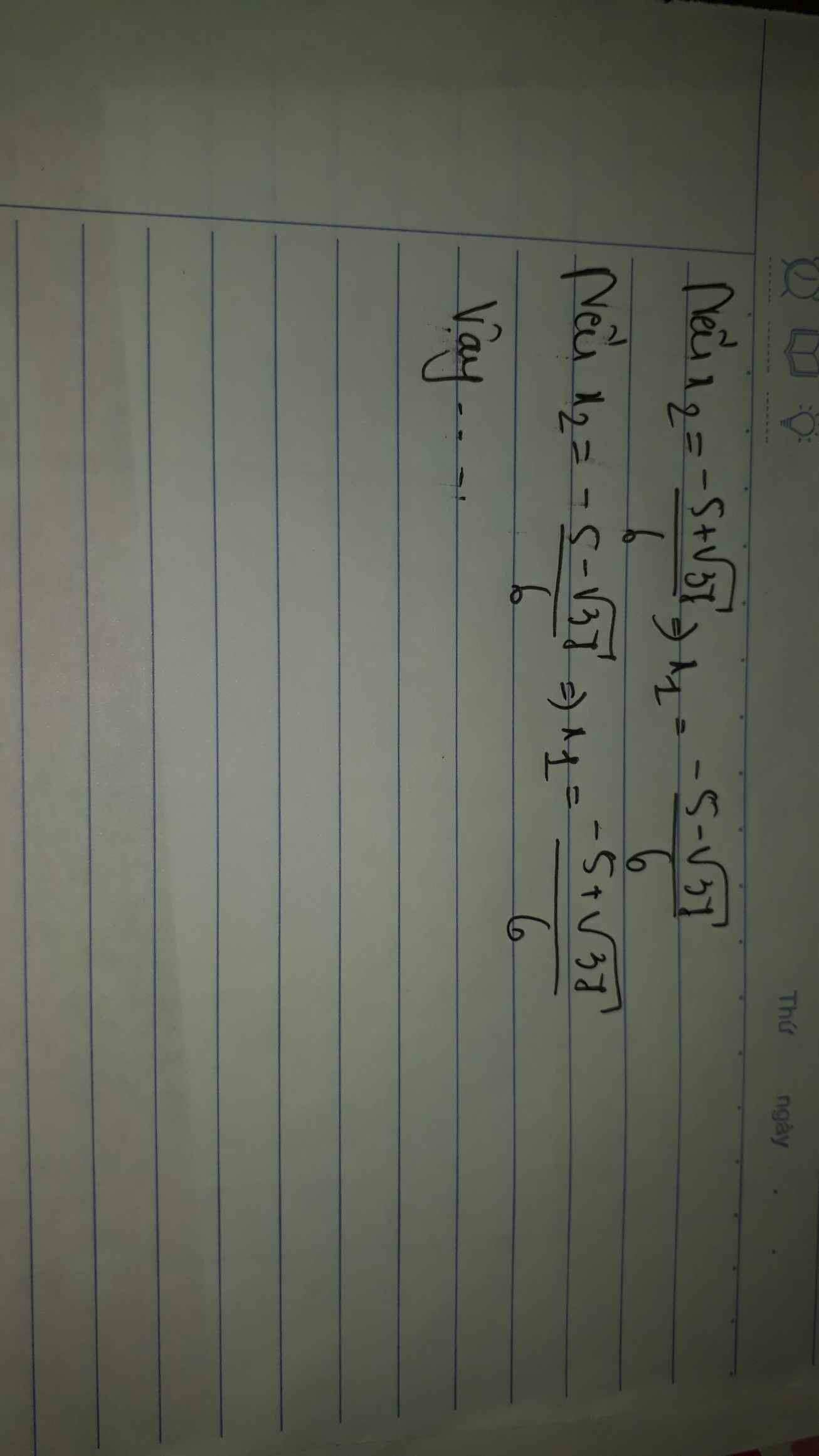
\(\text{Δ}=\left(2m-6\right)^2-4\left(m^2+3m+2\right)\)
\(=4m^2-24m+36-4m^2-12m-8=-36m+28\)
Để phương trình có hai nghiệm thì -36m+28>=0
=>-36m>=-28
hay m<=7/9
Theo đề, ta có:
\(\left(x_1+x_2\right)^2-2x_1x_2=100\)
\(\Leftrightarrow\left(\dfrac{2m-6}{m+1}\right)^2-2\cdot\dfrac{m+2}{m+1}=100\)
\(\Leftrightarrow\dfrac{\left(2m-6\right)^2-2\left(m^2+3m+2\right)}{\left(m+1\right)^2}=100\)
\(\Leftrightarrow4m^2-24m+36-2m^2-6m-4=100\left(m+1\right)^2\)
\(\Leftrightarrow50\left(m+1\right)^2=m^2-15m+16\)
\(\Leftrightarrow50m^2+100m+50-m^2+15m-16=0\)
\(\Leftrightarrow49m^2+115m+34=0\)
\(\text{Δ}=115^2-4\cdot49\cdot34=6561\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{-115-81}{2\cdot49}=-2\left(nhận\right)\\m_2=\dfrac{-115+81}{2\cdot49}=-\dfrac{17}{49}\left(nhận\right)\end{matrix}\right.\)