Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tam thức bậc hai có \(\Delta'=m^2-m+4=m^2-2.\frac{1}{2}m+\frac{1}{4}-\frac{1}{4}+4=\left(m-\frac{1}{2}\right)^2+\frac{15}{4}>0\).
Suy ra phương trình (1) luôn có nghiệm với mọi m.
b) Theo Vi-et ta có:
\(x_1+x_2=2m,x_1.x_2=m-4\)
Điều kiển để \(x_1+x_2=\frac{x_1^2}{x_2}+\frac{x_2^2}{x_1}\)
\(\Leftrightarrow x_1+x_2=\frac{x_1^3+x_2^3}{x_1x_2}\)
\(\Leftrightarrow x_1+x_2=\frac{\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)}{x_1x_2}\)
\(\Leftrightarrow2m=\frac{\left(2m\right)^3-3\left(m-4\right).2m}{m-4}\)
\(\Leftrightarrow2m\left(m-4\right)=8m^3-6m^2+8m\) và \(m\ne4\)
\(\Leftrightarrow4m\left(2m^2-2m+3\right)=0\) và \(m\ne4\)
\(\Leftrightarrow m=0\)

Đặt t = x2 (t \(\ge\) 0). Khi đó, phương trình đã cho trở thành: t2 - 2(m2 + 2).t + m4 + 3 = 0 (*)
\(\Delta\)' = (m2 +2)2 - (m4 + 3) = m4 + 4m2 + 4 - m4 - 3 = 4m2 + 1 > 0
=> (*) luôn có 2 nghiệm phân biệt. Gọi hai nghiệm đó là t1; t2
Theo hệ thức Vi - et ta có: t1 + t2 = 2(m2 + 2) > 0
t1. t2 = m4 + 3 > 0
=> t1 > 0 và t2 > 0 (thỏa mãn điều kiện của t)
vậy (*) luôn có 2 nghiệm dương phân biệt => pt đã cho luôn có 4 nghiệm phân biệt x1; x2 ; x3; x4
trong đó x1; x2 thỏa mãn x12 = x22 = t1; x32 = x24 = t2 ; x1; x2 đối nhau ; x3; x4 đối nhau
=> \(x_1^2+x^2_2+x^2_3+x^2_4+x_1\cdot x_2\cdot x_3\cdot x_4=2t_1+2t_2+\left(-x_1^2\right).\left(-x_2^2\right)=2.\left(t_1+t_2\right)+t_1.t_2\)
= 2.2.(m2 + 2) + m4 + 3 = m4 + 4m2 + 11

xét pt \(x^2-\left(m-1\right)x-m^2+m-1=0\) \(\left(1\right)\)
từ (1) có \(\Delta=\left[-\left(m-1\right)\right]^2-4.\left(-m^2+m-1\right)\)
\(\Delta=m^2-2m+1+4m^2-4m+4\)
\(\Delta=5m^2-6m+5\)
\(\Delta=5\left(m^2-\frac{6}{5}m+1\right)\)
\(\Delta=5\left[m^2-2.\frac{3}{5}m+\frac{9}{25}-\frac{9}{25}+1\right]\)
\(\Delta=5\left[\left(m-\frac{3}{5}\right)^2+\frac{16}{25}\right]>0\forall m\)
\(\Rightarrow pt\left(1\right)\) luôn có 2 nghiệm phân biệt \(\forall m\)
ta có vi - ét \(\hept{\begin{cases}x_1+x_2=m-1\\x_1.x_2=-m^2+m-1\end{cases}}\)
theo bài ra \(\left|x_2\right|-\left|x_1\right|=2\)
\(\Leftrightarrow\left(\left|x_1\right|+\left|x_2\right|\right)=4\)
\(\Leftrightarrow x_1^2+x_2^2+2\left|x_1.x_2\right|=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2+2\left|x_1.x_2\right|=4\)
\(\Leftrightarrow\left(m-1\right)^2-2\left(-m^2+m-1\right)+2\left|x_1.x_2\right|=4\)
\(\Leftrightarrow m^2-2m+1+2m^2-2m+2+2\left|x_1.x_2\right|=4\)
\(\Leftrightarrow3m^2-4m+3+2\left|x_1.x_2\right|=4\)
cái này đến đây xét ra 2 trường hợp rồi đối chiếu với ĐKXĐ là xong

a) Phương trình \(x^2-2mx-2m-1=0\)có các hệ số a = 1; b = - 2m; c = - 2m - 1
\(\Delta=\left(-2m\right)^2-4\left(-2m-1\right)=4m^2+8m+4=4\left(m+1\right)^2\ge0\forall m\)
Vậy phương trình luôn có 2 nghiệm x1, x2 với mọi m (đpcm)
b) Theo Viète, ta có: \(x_1+x_2=2m;x_1x_2=-2m-1\)
Hệ thức \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{-5}{2}\Leftrightarrow2\left(x_1^2+x_2^2\right)=-5x_1x_2\)
\(\Leftrightarrow2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=-5x_1x_2\)hay \(2\left(4m^2+4m+2\right)=10m+5\Leftrightarrow8m^2-2m-1=0\)\(\Leftrightarrow\orbr{\begin{cases}m=\frac{1}{2}\\m=-\frac{1}{4}\end{cases}}\)
Vậy \(m=\frac{1}{2}\)hoặc \(m=-\frac{1}{4}\)thì phương trình có 2 nghiệm x1, x2 thỏa mãn\(\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{-5}{2}\)

Để PT có 2 nghiệm phân biệt thì
\(\Delta'=\left(m-2\right)^2-\left(m^2-2m+4\right)>0\)
\(\Leftrightarrow m< 0\)
Theo vi et ta có:
\(\hept{\begin{cases}x_1+x_2=-2m+4\\x_1.x_2=m^2-2m+4\end{cases}}\)
Theo đề bài thì
\(\frac{2}{x_1^2+x_2^2}-\frac{1}{x_1.x_2}=\frac{15}{m}\)
\(\Leftrightarrow\frac{2}{\left(x_1+x_2\right)^2-2x_1.x_2}-\frac{1}{x_1.x_2}=\frac{15}{m}\)
\(\Leftrightarrow\frac{2}{\left(-2m+4\right)^2-2\left(m^2-2m+4\right)}-\frac{1}{m^2-2m+4}=\frac{15}{m}\)
\(\Leftrightarrow\frac{1}{m^2-6m+4}-\frac{1}{m^2-2m+4}=\frac{15}{m}\)
\(\Leftrightarrow15m^4-120m^3+296m^2-480m+240=0\)
Với m < 0 thì VP > 0
Vậy không tồn tại m để thỏa bài toán.

Đk pt có 2 nghiêm pb
\(\Delta=a^2-4>0\)
=>\(a^2>4\)
=>\(\orbr{\begin{cases}a>2\\a< -2\end{cases}}\)
theo Đly Vi-et, ta có x1+x2=-a
x1.x2=1
\(\frac{x_1^2}{x_2^2}+\frac{x_2^2}{x_1^2}=\frac{x_1^4+x_2^4}{x_1^2.x_2^2}=\frac{\left(x_1^2+x_2^2\right)^2-2x_1^2x_2^2}{1}=\left(\left(x_1+x_2\right)^2-2x_1x_2\right)^2-2=\left(a^2-2\right)^2-2\)
=>(a2-2)2-2 >7
=>(a2-2)2 >9
=>\(\orbr{\begin{cases}a^2-2>3\\a^2-2< -3\end{cases}=>\orbr{\begin{cases}a^2>5\\a^2< -1\left(loai\right)\end{cases}=>\orbr{\begin{cases}a>\sqrt{5}\\a< -\sqrt{5}\end{cases}}}\left(tmdk\right)}\)
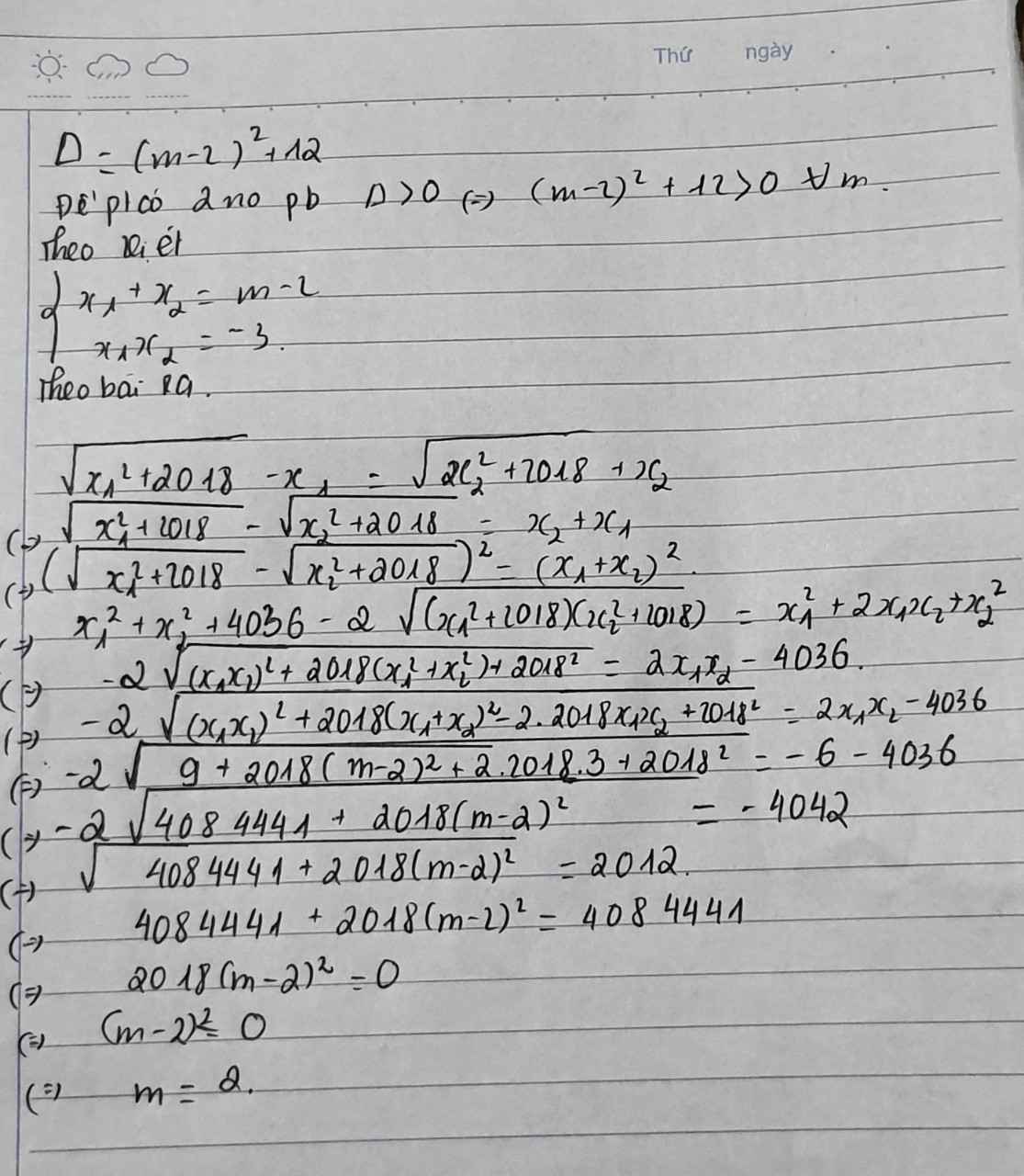
\(ac=-3< 0\Rightarrow\) pt đã cho luôn có 2 nghiệm pb trái dấu với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-3\end{matrix}\right.\)
\(\dfrac{x_1}{x_2^2}+\dfrac{x_2}{x_1^2}=m-1\Leftrightarrow\dfrac{x_1^3+x_2^3}{\left(x_1x_2\right)^2}=m-1\)
\(\Leftrightarrow\dfrac{\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)}{9}=m-1\)
\(\Leftrightarrow8\left(m-1\right)^3+18\left(m-1\right)=9\left(m-1\right)\)
\(\Leftrightarrow\left(m-1\right)\left[8\left(m-1\right)^2+9\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\\8\left(m-1\right)^2+9=0\left(vô-nghiệm\right)\end{matrix}\right.\)