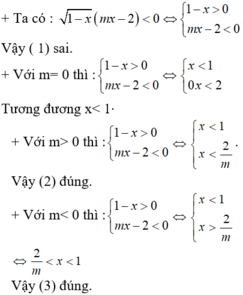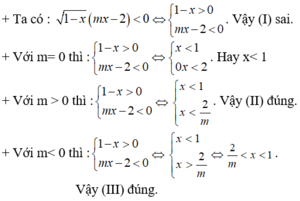Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \(\Delta\) = b2 - 4ac = (-m)2 - 4(2m - 4)
= m2 - 8m + 16 = ( m - 4 )2
Ta có: ( m - 4 )2 \(\ge\) 0
=> Pt luôn có nghiệm
b) Vì phương trình luôn có nghiệm nên áp dụng định lí Ta- lét:
\(\left\{{}\begin{matrix}x_1+x_2=\frac{-b}{a}==m\\x_1x_2=2m-4\end{matrix}\right.\)
Xét phương trình: x12 + x22 - 9
= x12 + x22 + 2x1x2 - 2x1x2 - 9
= (x1 + x2)2 - 2x1x2 - 9
= (-m)2 - 2(2m - 4) - 9
= m2 - 4m + 8 - 9
= m2 - 4m - 1 = m2 - 4m + 4 - 5
= (m - 2)2 - 5
Xét (m - 2)2 \(\ge\) 0
=> (m - 2)2 - 5 \(\ge\) -5
Dấu " =" xảy ra khi m - 2 = 0
<=> m = 2
\(\Delta=m^2-8m+16=\left(m-4\right)^2\ge0\Rightarrow\) pt luôn có nghiệm
Khi đó theo Viet \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=2m-4\end{matrix}\right.\)
\(A=x_1^2+x_2^2-9=\left(x_1+x_2\right)^2-2x_1x_2-9\)
\(A=m^2-2\left(2m-4\right)-9\)
\(A=m^2-4m-1\)
\(A=\left(m-2\right)^2-5\ge-5\)
\(\Rightarrow A_{min}=-5\) khi \(m=-2\)

Vì \(x_2\)là nghiệm của phương trình
=> \(x_2^2-5x_2+3=0\)
=> \(x_2+1=x^2_2-4x_2+4=\left(x_2-2\right)^2\)
Theo viet ta có
\(\hept{\begin{cases}x_1+x_2=5\\x_1x_2_{ }=3\end{cases}}\)=> \(x_1^2+x_2^2=19\)
Khi đó
\(A=||x_1-2|-|x_2-2||\)
=> \(A^2=\left(x^2_1+x_2^2\right)-4\left(x_1+x_2\right)+8-2|\left(x_1-2\right)\left(x_2-2\right)|\)
=> \(A^2=19-4.5+8-2|3-2.5+4|=1\)
Mà A>0(đề bài)
=> A=1
Vậy A=1

Pt đã cho có 3 nghiệm pb khi nó có một nghiệm bằng 0
\(\Rightarrow m^2-1=0\Rightarrow m=\pm1\)
- Với \(m=1\Rightarrow-x^2=0\) chỉ có 1 nghiệm (ktm)
- Với \(m=-1\Rightarrow-2x^4+x^2=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\pm\frac{\sqrt{2}}{2}\end{matrix}\right.\) (t/m)
Vậy \(m=-1\)

* Nếu m= 0 thì bất phương trình đã cho trở thành:
0x < 0( luôn đúng với mọi x).
* Nếu m= 1 thì bất phương trình đã cho trở thành:
0x < 1 ( luôn đúng với mọi x)
Tập tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x là {0; 1}