Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(x^2-2\left(m-1\right)x+m^2+m+1=0\left(a=1;b=-2m+2;c=m^2+m+1\right)\)
\(\Delta=\left(-2m+2\right)^2-4\left(m^2+m+1\right)=4m^2+4-4m^2-4m-4=-4m< 0\)
Nếu \(-4m< 0\Leftrightarrow m>0\) chắc ĐK là vậy.
Theo hệ thức Vi et ta có : \(x_1+x_2=2m+2;x_1x_2=m^2+m+1\)
Theo bài ra ta có : \(x_1^2+x_2^2=4x_1x_2-2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4x_1x_2-2\) Thay vao ta có pt mới :
\(\Leftrightarrow\left(2m+2\right)^2-4\left(m^2+m+1\right)=4\left(m^2+m+1\right)-2\)
\(\Leftrightarrow4m+4-4m^2-m-1=4m^2+4m+4-2\)
\(\Leftrightarrow3m+3-4m^2=4m^2+4m+2\)
\(\Leftrightarrow-m+1-8m^2=0\) Ta có : \(\left(-1\right)^2-4\left(-8\right)=1+32=33>0\)
\(x_1=\frac{1-\sqrt{33}}{-16};x_2=\frac{1+\sqrt{33}}{-16}\)
Tớ ngu ! tớ nhận.
Sửa từ dòng 4 trở lên.
\(\Leftrightarrow4m^2+4-4m^2-m-1=4m^2+4m+4-2\)
\(\Leftrightarrow3-m=4m^2+4m+2\)
\(\Leftrightarrow3-m-4m^2-4m-2=0\)
\(\Leftrightarrow1-5m-4m^2=0\)Ta có : \(\left(-5\right)^2-4\left(-4\right)=25+16=41>0\)
\(x_1=\frac{5-\sqrt{41}}{-4};x_2=\frac{5+\sqrt{41}}{-4}\)

\(\Delta=\left(-m\right)^2-2.1.\left(m-1\right)\\ =m^2-2m+1\\ =\left(m-1\right)^2\)
Phương trình có hai nghiệm phân biệt :
\(\Leftrightarrow\Delta>0\\ \Rightarrow\left(m-1\right)^2>0\\ \Rightarrow m\ne1\)
Theo vi ét :
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(x^2_1+x^2_2=x_1+x_2\\ \Leftrightarrow x^2_1+x^2_2=m\\ \Leftrightarrow\left(x^2_1+2x_1x_2+x_2^2\right)-2x_1x_2=m\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-m=0\\ \Leftrightarrow m^2-2\left(m-1\right)-m=0\\ \Leftrightarrow m^2-2m+2-m=0\\ \Leftrightarrow m^2-3m+2=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(loại\right)\\m=2\left(t/m\right)\end{matrix}\right.\)
Vậy \(m=2\)

Δ=5^2-4(m-3)
=25-4m+12=-4m+27
Để phương trình có 2 nghiệm thì -4m+27>=0
=>m<=27/4
Theo đề, ta có: x1-2<0 và x2-2>0
=>(x1-2)(x2-2)<0
=>x1x2-2(x1+x2)+4<0
=>m-3-2*(-5)+4<0
=>m+1+10<0
=>m<-11

viết lại câu hỏi khác đi, đề không rõ ràng X với x rồi . lung tung, dung công cụ soạn thảo đi nha bạn

c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4
Theo Vi-et ta có: 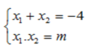
Ta có: x 1 2 + x 2 2 = 10 ⇔ x 1 + x 2 2 - 2x1x2 = 10
⇔ - 4 2 - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)
Vậy với m = 3 thì phương trình (1) có hai nghiệm thõa mãn: x 1 2 + x 2 2 = 10

a) Khi m = -5 ta được phương trình x2 + 4x - 5 = 0
Ta có a + b + c = 1 + 4 + (-5) = 0 nên phương trình có hai nghiệm phân biệt là x1 = 1; x2= c/a = (-5)/1 = -5
Tập nghiệm của phương trình S = {1; -5}
b) Δ' = 22 - m = 4 - m
Phương trình có nghiệm kép ⇔ Δ'= 0 ⇔ 4 - m = 0 ⇔ m = 4
c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4
Theo Vi-et ta có:
Ta có: x12 + x22 = 10 ⇔ (x1 + x2)2 - 2x1x2 = 10
⇔ (-4)2 - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)
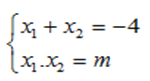
\(ac=-10< 0\Rightarrow\) phương trình luôn có 2 nghiệm pb trái dấu
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=-10\end{matrix}\right.\)
Kết hợp hệ thức Viet và đề bài:
\(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1-x_2=8\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-m+8}{2}\\x_2=\dfrac{-m-8}{2}\end{matrix}\right.\)
Thế vào \(x_1x_2=-10\)
\(\Rightarrow\left(\dfrac{-m+8}{2}\right)\left(\dfrac{-m-8}{2}\right)=-10\)
\(\Leftrightarrow m^2-64=-40\Rightarrow m^2=24\)
\(\Rightarrow m=\pm2\sqrt{6}\)