Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\frac{a-x}{b-y}=\frac{a}{b}\Rightarrow\left(a-x\right)b=\left(b-y\right)a\)
\(\Rightarrow ab-bx=ab-ay\Rightarrow bx=ay\)
\(\Rightarrow\frac{x}{y}=\frac{a}{b}\left(ĐPCM\right)\)

\(\dfrac{a-x}{b-y}=\dfrac{a}{b}\)
\(\Rightarrow\left(a-x\right).b=\left(b-y\right).a\)
\(\Rightarrow ab-xb=ba-ya\)
\(\Rightarrow xb=ya\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{x}{y}\) (đpcm)

Bài 1:
a) \(\dfrac{x^2}{6}=\dfrac{24}{25}\)
\(\Leftrightarrow x^2.25=6.24\)
\(\Leftrightarrow x^2.25=144\)
\(\Leftrightarrow x^2=144:25\)
\(\Leftrightarrow x^2=5,76\)
\(\Leftrightarrow x=2,4\)
b) \(\dfrac{x-1}{x+5}=\dfrac{6}{7}\)
\(\Leftrightarrow7\left(x-1\right)=6\left(x+5\right)\)
\(\Leftrightarrow7x-7=6x+30\)
\(\Leftrightarrow7x=6x+30+7\)
\(\Leftrightarrow7x=6x+37\)
\(\Leftrightarrow7x-6x=37\)
\(\Leftrightarrow x=37\)
c) \(\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\)
\(\Leftrightarrow\left(x-2\right)\left(x+7\right)=\left(x+4\right)\left(x-1\right)\)
\(\Leftrightarrow\left(x-2\right).x+\left(x-2\right).7=\left(x+4\right).x-\left(x+4\right)\)
\(\Leftrightarrow x^2-2x+7x-14=x^2+4x-x-4\)
\(\Leftrightarrow x^2+5x-14=x^2+3x-4\)
\(\Leftrightarrow x^2+5x-14+4-3x-x^2=0\)
\(\Leftrightarrow\left(x^2-x^2\right)+\left(5x-3x\right)-\left(14-4\right)=0\)
\(\Leftrightarrow2x-10=0\)
\(\Leftrightarrow2x=10\)
\(\Leftrightarrow x=10:2=5\)
Bài 2:
\(\dfrac{x}{7}=\dfrac{y}{13}\) và \(x+y=40\)
Ta có: \(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=\dfrac{40}{20}=2\)
Do đó \(\left\{{}\begin{matrix}\dfrac{x}{7}=2\Rightarrow x=14\\\dfrac{y}{13}=2\Rightarrow y=26\end{matrix}\right.\)
Vậy \(x=14;y=26\)

a, b, c là ba số nguyên tố khác nhau.
Ta có [a, b]= a.b, [b, c]= b.c, [c.a]= c.a
Do đó \(\dfrac{1}{\left[a,b\right]}+\dfrac{1}{\left[b,c\right]}+\dfrac{1}{[c,a]}=\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\)
Ta có: \(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\le\dfrac{1}{2.3}+\dfrac{1}{3.5}+\dfrac{1}{5.2}\)
mả \(\dfrac{1}{2.3}+\dfrac{1}{3.5}+\dfrac{1}{5.2}=\dfrac{5+2+3}{30}=\dfrac{1}{3}\).
Do đó \(\dfrac{1}{\left[a,b\right]}+\dfrac{1}{\left[b,c\right]}+\dfrac{1}{\left[c,a\right]}\le\dfrac{1}{3}\).

a)Ta có:\(\dfrac{1}{b}-\dfrac{1}{b+1}=\dfrac{b+1-b}{b\left(b+1\right)}=\dfrac{1}{b^2+b}< \dfrac{1}{b^2}\)(do b>1)
\(\dfrac{1}{b-1}-\dfrac{1}{b}=\dfrac{b-b+1}{\left(b-1\right)b}=\dfrac{1}{b^2-b}>\dfrac{1}{b^2}\)(do b>1)
b)Áp dụng từ câu a
=>\(\dfrac{1}{2}-\dfrac{1}{3}< \dfrac{1}{2^2}< \dfrac{1}{1}-\dfrac{1}{2}\)
\(\dfrac{1}{3}-\dfrac{1}{4}< \dfrac{1}{3^2}< \dfrac{1}{2}-\dfrac{1}{3}\)
.........................
\(\dfrac{1}{9}-\dfrac{1}{10}< \dfrac{1}{9^2}< \dfrac{1}{8}-\dfrac{1}{9}\)
=>\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}< S< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}\)
=>\(\dfrac{1}{2}-\dfrac{1}{10}< S< 1-\dfrac{1}{9}\)
=>\(\dfrac{2}{5}< S< \dfrac{8}{9}\)(đpcm)

AD tích chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{a+b+c}{b+c+d}\)
\(\Rightarrow\left(\dfrac{a+b+c}{b+c+d}\right)^3=\dfrac{a+b+c}{b+c+d}.\dfrac{a+b+c}{b+c+d}.\dfrac{a+b+c}{b+c+d}=\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{d}=\dfrac{a}{d}\)
\(\Rightarrow DPCM\)

Câu 2:
\(\Leftrightarrow x\left(\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+...+\dfrac{1}{78}\right)=\dfrac{220}{39}\)
\(\Leftrightarrow2x\left(\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{156}\right)=\dfrac{220}{39}\)
\(\Leftrightarrow x\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{12}-\dfrac{1}{13}\right)=\dfrac{110}{39}\)
\(\Leftrightarrow x\cdot\dfrac{10}{39}=\dfrac{110}{39}\)
=>x=11
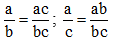
\(\dfrac{a-x}{b-y}=\dfrac{a}{b}\)
\(\Rightarrow\dfrac{a-x}{a}=\dfrac{b-y}{b}\)
\(\Rightarrow1-\dfrac{x}{a}=1-\dfrac{y}{b}\)
\(\Rightarrow\dfrac{x}{a}=\dfrac{y}{b}\)
\(\Rightarrow\dfrac{x}{y}=\dfrac{a}{b}\)