Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Hai hàm số có đồ thị // với nhau khi
\(\hept{\begin{cases}m-2=1\\3\ne0\end{cases}}\Leftrightarrow m=3\)
b/ Tọa độ giao điểm 2 đường thẳng là nghiệm của hệ
\(\hept{\begin{cases}y=x+3\\y=2x+1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=5\end{cases}}\)
c/ Gọi điểm mà đường thẳng luôn đi qua là M(a,b) ta thế vào hàm số được
\(b=ma+3\)
\(\Leftrightarrow ma+3-b=0\)
Để phương trình này không phụ thuôc m thì
\(\hept{\begin{cases}a=0\\3-b=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=0\\b=3\end{cases}}\)
Tọa độ điểm cần tìm là M(0, 3)
d/ Ta có khoản cách từ O(0,0) tới (d) là 1
\(\Rightarrow=\frac{\left|0-0m-3\right|}{\sqrt{1^2+m^2}}=\frac{3}{\sqrt{1+m^2}}=1\)
\(\Leftrightarrow\sqrt{1+m^2}=3\)
\(\Leftrightarrow m^2=8\)
\(\Leftrightarrow\orbr{\begin{cases}m=2\sqrt{2}\\m=-2\sqrt{2}\end{cases}}\)

Tham khảo:


c. Giao điểm thứ hai của đồ thị có hoành độ bằng -3 và tung độ bằng 9. Ta có : B(-3 ; 9).

Bài 1: b) Ptrình hoành độ giao điểm:
\(2x^2-4x=0\Leftrightarrow2x\left(x-2\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=0\\y=8\end{matrix}\right.\)
Vậy hai đồ thị giao tại (0;0);(2;8).
Bài 1:
a) Hình vẽ:

b) Gọi $(x_0,y_0)$ là giao điểm của 2 đồ thị. Khi đó:
\(\left\{\begin{matrix} y_0=2x_0^2\\ y_0=4x_0\end{matrix}\right.\Rightarrow 2x_0^2=4x_0\)
\(\Leftrightarrow 2x_0^2-4x_0=0\Leftrightarrow 2x_0(x_0-2)=0\Rightarrow x_0=0\) hoặc \(x_0=2\)
Với \(x_0=0\Rightarrow y_0=4x_0=0\). Ta có giao điểm $(0,0)$
Với \(x_0=2\Rightarrow y_0=4x_0=8\). Ta có giao điểm $(2,8)$

a, thay x=2, y=-2 vào y=ax^2 ta đc
-2=a*2^2
-2=4a
a=-1/2
phương trình trở thành
y=-1/2x^2
lập bảng vs x có 5 gt: -2;-1;0;1;2
tìm y theo x
kẻ đc bảng
b,gọi phương trình đường thẳng D là y=ax+b
do D song song với đường thẳng y=2x nên ta được:
a=2 và b khác 0
thay a=2 pt D trở thành
y=2x+b
do D tiếp xúc vs P nên ta đc
-1/2x^2=2x+b
-1/2x^2-2x-b=0
ta có: đenta'=1-b/2
mà D tiếp xúc vs P nên đenta' =0
1-b/2=0
b=2
vậy (D):y=2x+2
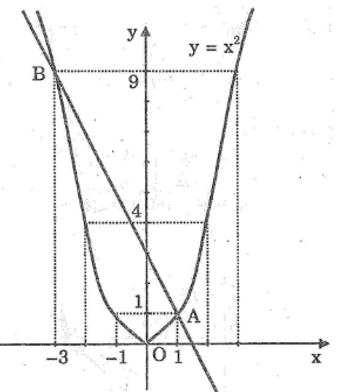
Vì đồ thị hàmsố P đi qua A(-2;1) nên ta thay x=-2, y=1 vào P . ta được
\(1=a\cdot\left(-2\right)^2=a\cdot4\Leftrightarrow a=\frac{1}{4}\)
Thay a=1/4 vào P ta có:\(y=\frac{1}{4}\cdot x^2\)
Xét phương trình hoành độ giao điểm của P và d ta có
\(\frac{1}{4}\cdot x^2=2x+1\Leftrightarrow\frac{1}{4}\cdot x^2-2x-1=0\)*
giải phuong trình * để tìm ra x1, y1 và cặp x2, y2