Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c. Gọi DK là đường cao của \(\Delta DPQ\)\(\left(K\in PQ\right)\)
F là giao điểm của DK với (O)\(\left(F\ne D\right)\)
Ta có: \(\widehat{OCA}=\widehat{OKA}=90^0\)
\(\Rightarrow\)Tứ giác OCAK nội tiếp.
\(\Rightarrow\widehat{COK}+\widehat{CAK}=180^0\)
Mà \(\widehat{COK}+\widehat{COF}=180^0\)
\(\Rightarrow\widehat{CAK}=\widehat{COF}\)
\(\Rightarrow\widehat{CAK}=180^0-\left(\widehat{FCO}+\widehat{CFO}\right)=180^0-2\widehat{FCO}\)(Vì \(\Delta OFC\) cân tại O (OC=OF))
Ta có: \(\widehat{FCD}=90^0\)(góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow\widehat{FCO}+\widehat{OCD}=90^0\)
Lại có:\(\widehat{OCA}=\widehat{OCD}+\widehat{ACD}=90^0\)(tính chất tiếp tuyến)
\(\Rightarrow\widehat{FCO}=\widehat{ACD}\)
\(\Delta CAQ\) có: \(\widehat{CAQ}+\widehat{ACD}+\widehat{AQC}=180^0\)
\(\Rightarrow180^0-2\widehat{FCO}+\widehat{FCO}+\widehat{AQC}=180^0\)
\(\Leftrightarrow\widehat{AQC}=\widehat{FCO}=\widehat{ACQ}\)
\(\Rightarrow\Delta CAQ\)cân tại A.
Lại có: AC=AB (Tính chất tiếp tuyến)
AB=AP(\(\Delta ABP\) cân tại A)
\(\Rightarrow AP=AC=AB=AQ\)
\(\Delta CPQ\)có: \(A\in PQ;AP=AC=AQ\)
\(\Rightarrow\Delta CPQ\)vuông tại C.
=>F,C,P thẳng hàng.
=> PC là đường cao của \(\Delta DPQ\)(\(C\in DQ\))
=> F là trực tâm của \(\Delta DPQ\)
=> F trùng với H.
Mà F thuộc (O)
=> H thuộc (O)

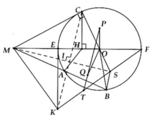
a, HS tự chứng minh
b, MH.MO = MA.MB ( = M C 2 )
=> ∆MAH:∆MOB (c.g.c)
=> M H A ^ = M B O ^
M B O ^ + A H O ^ = M H A ^ + A H O ^ = 180 0
=> AHOB nội tiếp
c, M K 2 = ME.MF = M C 2 Þ MK = MC
∆MKS = ∆MCS (ch-cgv) => SK = SC
=> MS là đường trung trực của KC
=> MS ^ KC tại trung của CK
d, Gọi MS ∩ KC = I
MI.MS = ME.MF = M C 2 => EISF nội tiếp đường tròn tâm P Þ PI = PS. (1)
MI.MS = MA.MB (= M C 2 ) => AISB nội tiếp đường tròn tâm Q Þ QI = QS. (2)
Mà IT = TS = TK (do DIKS vuông tại I). (3)
Từ (1), (2) và (3) => P, T, Q thuộc đường trung trực của IS => P, T, Q thẳng hàng
ko thấy ai trả lời, chắc ko ai biết làm bài này
Tr oii câu này ra lâu lắm rồi mà chả có ai trả lời. Chắc bây giờ bn í tầm 17 tuổi r ^_^