Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho đường tròn tâm OO đường kính MNMN và AA là một điểm trên đường tròn (O)(O), (AA khác MM và AA khác NN). Lấy một điểm II trên đoạn thẳng ONON (II khác OO và II khác NN). Qua II kẻ đường thẳng (d)(d) vuông góc với MNMN. Gọi PP, QQ lần lượt là giao điểm của AMAM, ANAN với đường thẳng (d)(d). Gọi KK là điểm đối xứng của NN qua điểm II. Chứng minh góc PMK = IQN\widehat{PMK}=\widehat{IQN}
và tứ giác MPQKMPQK nội tiếp đường tròn.
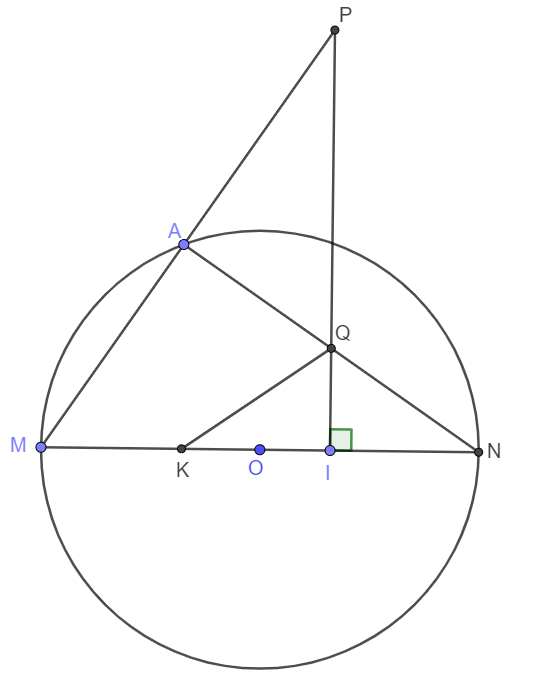
Xét 2 tam giác AMN và IQN có :
góc A= goc QIN= 90 (gt)
=> goc M= IQN= 90 - goc N (đpcm)
Xet 2 tam giác IQK và IQN có:
IQ chung
vì K là điểm đối xứng của NN qua điểm II
=> IK =IN
góc QIK = QIN=90
=> 2 tam giác IQK = IQN (c.g.c)
=> góc IQK=IQN=PQA=PMK
trong đó góc PQK + IQN = 180
=> góc PQK + PMK = 180
=> đpcm