Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

MÌNH THAM KHẢO NHÉ
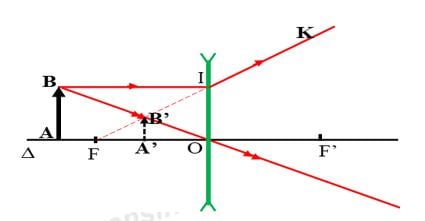
a) Xét △ABO và △A′B′O có:
ABOˆ=A′B′Oˆ=900
BOAˆ=B′OA′ˆ (hai góc đối đỉnh)
⇒ Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
⇒ \(\frac{A'B'}{AB}=\frac{B'O}{BO}\)
⇒ Độ phóng đại ảnh \(k=\frac{A'B'}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự: Hai tam giác A'B'F' và IOF' là hai tam giác đồng dạng
⇒\(\text{ }\frac{B'F'}{OF'}=\frac{A'B'}{IO}=\frac{d'}{d}\)
Áp dụng tính chất của tỉ lệ thức: \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)
⇒\(\frac{1}{f}=\frac{1}{d}=\frac{1}{f'}\)
CÓ MẤY CÁI KÍ HIỆU GÓC, MÌNH KHÔNG BIẾT VIẾT, BẠN THÔNG CẢM
a) Xét \(\Delta ABO\) và \(\Delta A'B'O'\)
\(ABO=A'B'O=90^0\)
\(BOA=B'O'A\)( hai góc đối đỉnh )
\(\Rightarrow\)Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
\(\Rightarrow\frac{A'B}{AB}=\frac{B'O}{BO}\)
\(\Rightarrow\)Độ phóng đại ảnh : \(k=\frac{A'B}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự : Hai tam giác A'B'F và IOF' là hai tam giác đồng dạng
\(\Rightarrow\frac{B'F'}{OF}=\frac{A'B}{TO}=\frac{d'}{d}\)
Dựa vào tính chất của tỉ lệ thức : \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)

sao đang xét tam giác S'IA với S'I'A' lại có tỉ số BA/B'A' vậy ạ

tóm tắt:
TNPK có \(\left|f\right|=12cm;\) vật AB cao :h = 2cm ; d=8cm
a, dựng ảnh:
tính chất ảnh : ảnh này là ảo ảnh;nhỏ hơn vật , cùng chiều với vật

bài 1:
a/ Quãng đường đi trong 5s đầu: S5 = v0t5 + at52
Quãng đường đi trong 6s:S6 = v0t6 + at62
Quãng đường đi trong giây thứ 6:
S = S6 - S5 = 14 a = 2m/s2
b/ S20 = v0t20 + at202 = 460m
bài 4:
S1 = v0t1 + at12
4.v01 + 8a = 24 (1)
S2 = v01t2 + at22
4.v01 + 8a = 64 (2)
Mà v02 = v1 = v01 + at2 (3)
Giải (1), (2), (3) ta được : v01 = 1m/s, a = 2,5m/s2
2 bài còn lại ko bt lm

a. áp dụng hệ thức lượng ta có:
\(MH^2=AH.BH\Rightarrow BH=\frac{4^2}{2}=8cm\)
\(\Rightarrow\hept{\begin{cases}AB=AH+HB=2+8=10cm\\MA=\sqrt{AH.AB}=\sqrt{20}cm\end{cases}}\)
b. ta có :
\(\frac{1}{MA^2}+\frac{1}{MB^2}\ge\frac{4}{MA^2+MB^2}=\frac{4}{AB^2}=const\)
dấu bằng xảy ra khi \(MA=MB\Rightarrow M\text{ nằm chính giữa cung tròn AB}\)