Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đơn giản là em đang xem một lời giải sai. Việc khẳng định $P\leq 0$ hoặc $P>0$ rồi kết luận hàm số không có GTLN là sai.
Bởi vậy những câu hỏi ở dưới là vô nghĩa.
Việc gọi $P$ là hàm số lên lớp cao hơn em sẽ được học, còn bây giờ chỉ cần gọi đơn giản là phân thức/ biểu thức.
Hàm số, có dạng $y=f(x)$ biểu diễn mối liên hệ giữa biến $x$ với biến phụ thuộc $y$. Mỗi giá trị của $x$ ta luôn xác định được một giá trị tương ứng của $y$.
$P=AB=\frac{\sqrt{x}}{\sqrt{x}-1}=1+\frac{1}{\sqrt{x}-1}$
Để $P_{\max}$ thì $\frac{1}{\sqrt{x}-1}$ max
Điều này xảy ra khi $\sqrt{x}-1$ min và có giá trị dương
$\Leftrightarrow x>1$ và $x$ nhỏ nhất
Trong tập số thực thì em không thể tìm được số lớn hơn 1 mà nhỏ nhất được. Như kiểu $1,00000000000000000000....$ (vô hạn đến không biết khi nào thì kết thúc)
Do đó $P$ không có max
Min cũng tương tự, $P$ không có min.

=\(\sqrt{\left(5+2\sqrt{6}\right)+\left(2\sqrt{10}+2\sqrt{15}\right)+5}\)
=\(\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2+2\sqrt{5}\left(\sqrt{2}+\sqrt{3}\right)+\left(\sqrt{5}\right)^2}\)
=\(\sqrt{\left(\sqrt{3}+\sqrt{2}+\sqrt{5}\right)^2}\)
=\(\sqrt{3}+\sqrt{2}+\sqrt{5}\)

Mình nghĩ với pt tổng quát: \(ax^2+bx+c=0\) có \(\Delta=b^2-4ac\)
Nếu như vậy thì: \(1.x^2+6x+m\) có \(\Delta=6^2-4m\)chứ?
Riêng mình thì bài này mình dùng delta phẩy cho lẹ:
Lời giải
Để pt \(x^2+6x+m=0\) có 2 nghiệm phân biệt thì:
\(\Delta'=\left(\frac{b}{2}\right)^2-ac=3^2-m>0\)
\(\Leftrightarrow m< 9\)

Câu trả lời là không. Và lời giải khá đơn giản. Thay dấu cộng bằng số 1 và dấu trừ bằng - 1. Xét tích tất cả các số trên bảng vuông. Khi đó, qua mỗi phép biến đổi, tích này không thay đổi (vì sẽ đổi dấu 4 số). Vì vậy, cho dù ta thực hiện bao nhiêu lần, từ bảng vuông (1, 15) sẽ chỉ đưa về các bảng vuông có số lẻ dấu -, có nghĩa là không thể đưa về bảng có toàn dấu cộng.
Bạn tham khảo nha

n là số nguyên dương
Bình phương hai vế, ta được:
\(\left(\sqrt{n+2}-\sqrt{n+1}\right)^2=n+2+n+1-2\sqrt{\left(n+2\right)\left(n+1\right)}\) \(=2n+3-2\sqrt{\left(n+2\right)\left(n+1\right)}\)
\(\left(\sqrt{n+1}-\sqrt{n}\right)^2=n+1+n-2\sqrt{n\left(n+1\right)}\) \(=2n+1-2\sqrt{n\left(n+1\right)}\)
Ta có: \(\left(n+2\right)\left(n+1\right)>n\left(n+1\right)\Rightarrow2\sqrt{\left(n+2\right)\left(n+1\right)}>2\sqrt{n\left(n+1\right)}\)
Mà 2n + 3 > 2n + 1
\(\Rightarrow2n+3-2\sqrt{\left(n+2\right)\left(n+1\right)}>2n+1-2\sqrt{n\left(n+1\right)}\)
=> ( √n+2 - √n+1)^2 > ( √n-1 - √n)^2
=> √n+2 - √n+1 > √n-1 - √n
P/s: Em làm còn sai nhiều, mong mọi người góp ý, đừng chọn sai cho em. Em cảm ơn

Khi đặt tụ 19 lá dưới tụ còn lại thì lá bài của đối phương sẽ là lá bài thứ 34 (tụ ở trên có 33 lá)
nếu theo khả năng 2 : đếm đến 1 mà số đếm vẫn khác....... thì số bài đã lấy ra sẽ đúng 33 lá
Khi đó lá bài tiếp theo (úp) sẽ là lá bài của đối phương : lá thứ 34.
p/s: làm thử 1 trường hợp vì không chắc .-.

Bài 1:
Nếu chị nhớ không nhầm thì phải là \(\left[\begin{matrix} \frac{1}{2}\leq x< 2\\ 0< x<\frac{1}{2}\end{matrix}\right.\)
Tức là $x$ nhận các khoảng giá trị sau:
\(0< x< \frac{1}{2}\); \(x=\frac{1}{2}\); \(\frac{1}{2}< x< 2\)
Vậy có nghĩa $0< x< 2$ (rất dễ hiểu mà????)
Bài 2:
Ngoặc nhọn dùng khi muốn biểu thị hai/ nhiều phương trình/ bất phương trình đồng thời xảy ra cùng một lúc
Ngoặc vuông dùng khi muốn biểu thị cái này hoặc cái kia xảy ra.
Bài trên phải dùng ngoặc vuông là sao em? Ngoặc nhọn thường xuất hiện trong bài toán giải hệ phương trình, bất phương trình. Còn ngoặc vuông thì thường dùng kết luận nghiệm của pt/ bpt.
Kết hợp điều kiện thì dùng ngoặc nhọn. Ví dụ $\sqrt{x+1}+\sqrt{2-x}$ thì việc $x+1\geq 0$ và $2-x\geq 0$ phải đồng thời xảy ra cùng lúc.
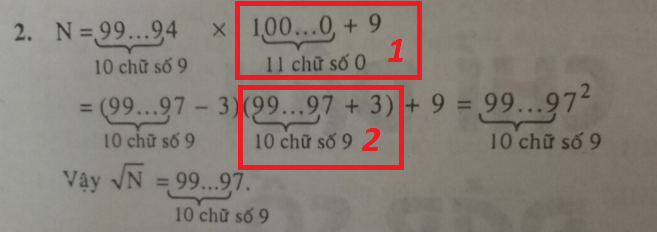
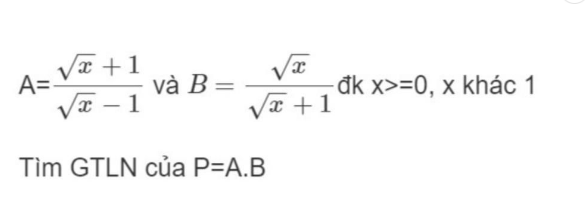

Tất cả những vấn đề em hỏi đều thuộc lý thuyết phân tích cấu tạo số cơ bản. Tất nhiên, lời giải sẽ có 1 chút tắt (không đáng kể).
Tip: Em chịu khó viết ra nháp từng bước một và đọc kỹ. Nếu thấy số dài mà không hiểu vì sao người ta làm vậy, em thử với bộ số nhỏ hơn có phong cách tương tự (ví dụ 994009)
\(\underbrace{999....9}_{10} 4\underbrace{000..0}_{10}9=\underbrace{999....9}_{10} 4\underbrace{00...0}_{11}+9\)
\(=\underbrace{999....9}_{10}4\times 1\underbrace{00...0}_{11}+9\)
\(=(\underbrace{999....9}_{10}7-3)\times (\underbrace{99....9}_{10}7+3)-9\)
(em tưởng tượng 1000 có 3 chữ số 0 đằng sau, biểu diễn được thành 997+3 có 3-1=2 chữ số 9)