Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Có duy nhất một đường thẳng đi qua M song song với d
b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) vì hai đường thẳng song song đồng phẳng

Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
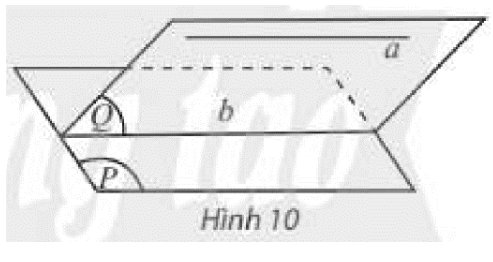
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia

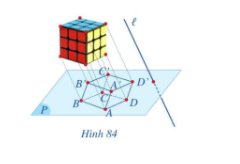
Trường hợp 1: Đặt rubik sao cho các cạnh bên của rubik song song hoặc trùng với đường thẳng ℓ.
Khi đó hình chiếu của rubik trên mp(P) là hình thoi.
Trường hợp 2: Đặt rubik sao cho các cạnh bên của rubik không song song hoặc trùng với đường thẳng ℓ.
Khi đó hình chiếu của rubik trên mp(P) là hình lục giác.
Hình ảnh của khối rubik qua phép chiếu song song lên mặt phẳng (P) theo phương l là hình hộp ABCD.A’B’C’D’

Đáp án B
Các cách xác định mặt phẳng đúng: 2; 4 ; 8
1. Đi qua 3 điểm phân biệt không thẳng hàng
3. Trong trường hợp 2 đường thẳng chéo nhau thì không thể xác định được mặt phẳng
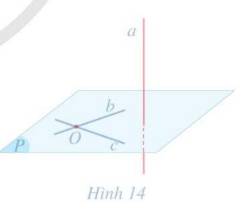
5. Song song với 2 đường thẳng cắt nhau Có vô số mặt phẳng như vậy.
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
6. Song song với 2 đường thẳng chéo nhau Có vô số mặt phẳng như vậy
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
7. Đi qua 1 điểm và song song với một đường thẳng cho trước. Có vô số mặt phẳng như vậy

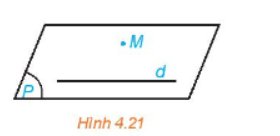
a: Có 1 đường duy nhất
b: Đường thẳng d cắt (P) tại 1 giao điểm

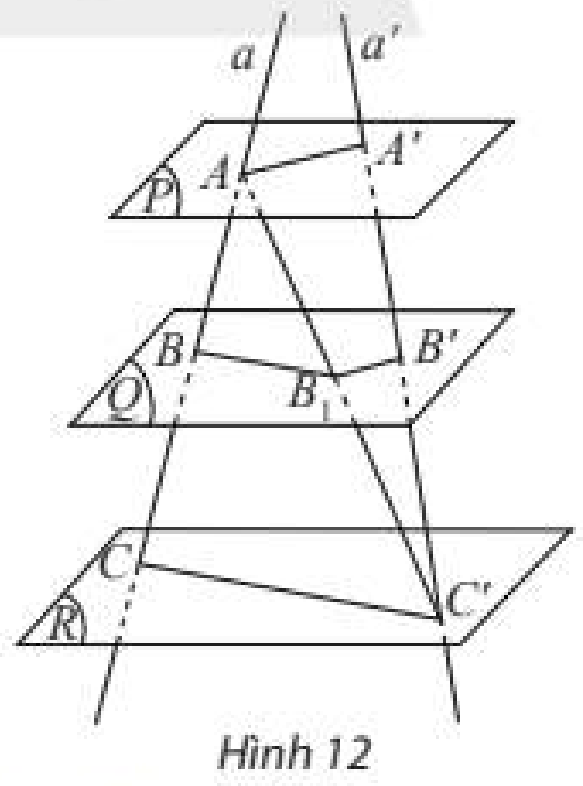
a) Ta có:
\(\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( {ACC'} \right) \cap \left( Q \right) = B{B_1}\\\left( {ACC'} \right) \cap \left( R \right) = CC'\end{array} \right\} \Rightarrow B{B_1}\parallel CC' \Rightarrow \frac{{AB}}{{BC}} = \frac{{A{B_1}}}{{{B_1}C'}}\left( 1 \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left( P \right)\parallel \left( Q \right)\\\left( {AA'C'} \right) \cap \left( Q \right) = B{B_1}\\\left( {AA'C'} \right) \cap \left( P \right) = AA'\end{array} \right\} \Rightarrow B{B_1}\parallel AA' \Rightarrow \frac{{A{B_1}}}{{{B_1}C'}} = \frac{{A'B'}}{{B'C'}}\left( 2 \right)\)
c) Từ (1) và (2) suy ra \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AB + BC}}{{A'B' + B'C'}} = \frac{{AC}}{{A'C'}}\)
Vậy \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\).
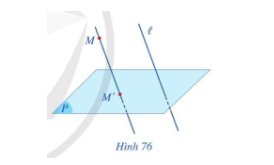

Qua mỗi điểm M trong không gian, có duy nhất một đường thẳng song song hoặc trùng với đường thẳng ℓ. Đường thẳng đó và mặt phẳng (P) có 1 điểm chung.