Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S=4\pi R^2=36\pi\Rightarrow R=3\) \(\Rightarrow OA=3\)
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) và \(OH=2\sqrt{2}\)
Pitago tam giác vuông OAH:
\(AH=\sqrt{OA^2-OH^2}=1\)
\(\Rightarrow AB=2AH=2\)

\(S=4\pi R^2=36\pi\Rightarrow R=3\)
\(\Rightarrow OB=R=3\)
Áp dụng định lý Pitago cho tam giác OAB:
\(AB=\sqrt{OA^2-OB^2}=\sqrt{5^2-3^2}=4\)

\(\widehat{MON}=180^0-\widehat{MAN}=120^0\)
\(S=4\pi R^2=36\pi\Rightarrow R=3\Rightarrow OM=ON=3\)
Áp dụng định lý hàm cos cho tam giác MON:
\(MN=\sqrt{OM^2+ON^2-2OM.ON.cos\widehat{MON}}=\sqrt{3^2+3^2-2.3.3.cos120^0}=3\sqrt{3}\)

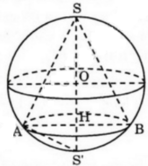
Gọi H là tâm mặt đáy của hình nón, O là tâm mặt cầu (S), đường thẳng IH cắt mặt cầu (S) tại điểm K.


Chọn C.
Dựa vào công thức diện tích mặt cầu và thể tích hình cầu, ta có:
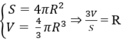

\(S=\dfrac{4}{3}\pi R^3=288\pi\Rightarrow R=6\)
Áp dụng định lý Pitago:
\(r=\sqrt{R^2-d^2}=\sqrt{6^2-\left(2\sqrt{5}\right)^2}=4\)

Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là:
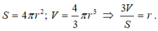
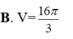
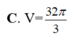
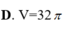
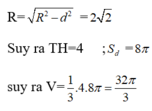
\(S=4\pi R^2=36\pi\Rightarrow R=3\)
\(V=\dfrac{4}{3}\pi R^3=36\pi\)