Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
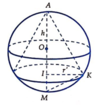
Kí hiệu như hình vẽ.
Ta thấy I K = r ' là bán kính đáy của hình chóp, A I = h là chiều cao của hình chóp.
Tam giác vuông tại K có IK là đường cao
⇒ I K 2 = A I . I M ⇒ r ' 2 = h . 2 r − h
Ta có V c o h p = 1 3 . π r ' 2 . h = 1 3 . π . h . h . 2 r − h = 4 3 π . h 2 . h 2 2 r − h .
Áp dụng bất đẳng thức Cauchy ta có
h 2 . h 2 . 2 r − h ≤ h 2 + h 2 + 2 r − h 3 27 = 8 r 3 27
⇔ V c h o p ≤ 4 3 π . 8 r 3 27 = 32 81 . π r 3
Dấu bằng xảy ra khi h 2 = 2 r − h ⇔ h = 4 r 3 . Vậy ta chọn A

Đáp án A
Vì hình trụ nội tiếp trong mặt cầu bán kính R cố định
⇒ R 2 = r 2 + h 2 2 = r 2 + h 2 4 ≥ 2 r 2 × h 2 4 = r h ⇒ r h = R 2
Diện tích xung quanh của hình trụ là: S x q = 2 πrh ≤ 2 πR 2
Dấu “=” xảy ra khi r 2 + h 2 4 = R 2 r 2 = h 2 4 ⇒ h = R 2 .

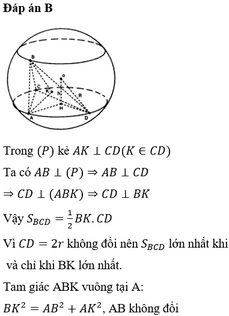
Chọn C.
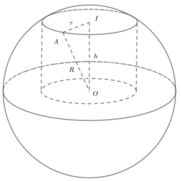
Phương pháp: Dựa vào dữ kiện bài toán lập hàm số và tìm giá trị lớn nhất, nhỏ nhất.

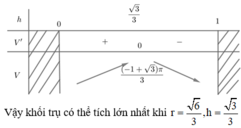

Đáp án C
Gọi r và h tương ứng là bán kính đáy và chiều cao của khối trụ
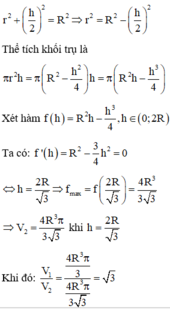
Ta có

Đáp án A
Vì hình trụ nội tiếp hình cầu S ⇒ R 2 = r 2 + h 2 2 ⇔ 4 r 2 + h 2 = 4 R 2
Diện tích xung quanh của hình trụ là S x q = 2 π r h = π .2 r . h ≤ π 2 r 2 + h 2 2 = π 4 r 2 + h 2 2 = 2 π R 2
Dấu “=” xảy ra khi và chỉ khi 2 r = h ⇒ 2 h 2 = 4 R 2 ⇔ h 2 = 2 R 2 ⇔ h = R 2
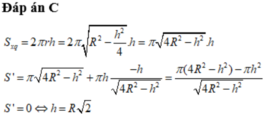
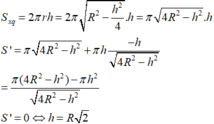
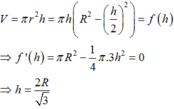
Đáp án A
Ký hiệu như hình vẽ. Đặt A B = B C = C D = D A = a ; S O = h
Suy ra S B = a 2 2 + h 2
Gọi M là trung điểm của SB
Trong (SBD) kẻ trung trực của SB cắt SO tại I
Vậy I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD. Suy ra I S = R .
Hai tam giác vuông SMI và SOB đồng dạng ⇒ S I S B = S M S O ⇒ R = a 2 + 2 h 2 4 h với 0 < h < 2 R . Suy ra a 2 = 2 h 2 R − h .
Thể tích V của khối chóp là:
V = 1 3 a 2 h = 1 3 2 h 2 2 R − h = 8 3 h 2 h 2 2 R − h ≤ 8 3 h 2 + h 2 + 2 R − h 3 3 = 64 R 3 81
Vậy GTLN của V bằng 64 R 3 81 đạt được khi h 2 = 2 R − h ⇔ h = 4 R 3
Suy ra a = 4 R 3 .