Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
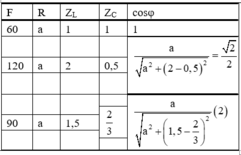
Dùng phương pháp chuẩn hóa:
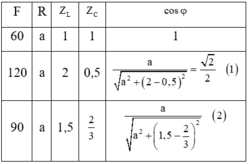
Giải (1) ta được: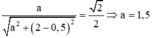 
Thay a=1,5 vào (2) ta có:
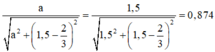
Đáp án B
+ Khi f = f 1 = f C → điện áp hiệu dụng trên tụ cực đại
Công suất tiêu thụ của toàn mạch P = P max cos 2 φ = 0 , 75 P max ⇒ cos 2 φ = 2 1 + n = n = 7 6 .
+ Khi f = f 2 = f 1 + 100 = f L
điện áp hiệu dụng trên cuộn cảm cực đại:
n = f L f C = f 1 + 100 f 1 = 7 6 ⇒ f 1 = 150 H z . Ghi chú: Với bài toán tần số góc biến thiên để điện áp hiệu dụng trên các phần tử cực đại, ta có thể áp dụng kết quả chuẩn hóa sau:
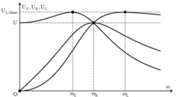
Ta để ý rằng khi tăng dần ω thì thứ tự cực đại của các điện áp là
ω C = X L → ω L = 1 L C → ω L = 1 C X
ω L ω C = ω R 2
Để đơn giản cho biểu thức ta tiến hành chuẩn hóa X = 1 và đặt n = ω L ω C = L C .
+ Khi U C max thì ω C = X L ⇒ Z L = X = 1 , n = L C = Z L Z C ⇒ Z C = n
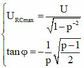
khi đó U C max = U 1 - n - 2 cos φ = 2 n + 1
+ Khi U L max thì ω L = 1 C X ⇒ Z C = X = 1 , n = L C = Z L Z C ⇒ Z L = n
khi đó U L max = U 1 - n - 2 cos φ = 2 n + 1
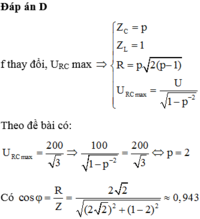
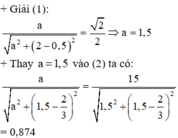
Khi f=f2=100Hz, công suất toàn mạch cực đại \(\Rightarrow \omega_2=\dfrac{1}{\sqrt{LC}}\)
\(\cos\varphi_1=\dfrac{R+r}{\sqrt{(R+r)^2+Z_L^2}}=0,6\)(1)
\(\cos\varphi_2=\dfrac{R+r}{\sqrt{(R+r)^2+(Z_L-Z_C)^2}}=0,8\)(2)
Đặt \(X=R+r\)
\((1)\Rightarrow X^2=0,36X^2+0,36Z_L^2\Rightarrow 0,64X^2=0,36Z_L^2\)(3)
\((2)\Rightarrow X^2=0,64X^2+0,64(Z_L-Z_C)^2\Rightarrow 0,36X^2=0,64(Z_L-Z_C)^2\)(4)
Từ (3) và (4) \(\Rightarrow\dfrac{0,36}{0,64}Z_L^2=\dfrac{0,64}{0,36}(Z_L-Z_C)^2\)
\(\Rightarrow \dfrac{0,36}{0,64}Z_L=|Z_L-Z_C|\)
TH1: \(\Rightarrow \dfrac{0,36}{0,64}Z_L=Z_L-Z_C\)\(\Rightarrow \dfrac{0,28}{0,64}Z_L=Z_C\)\(\Rightarrow \dfrac{0,28}{0,64}\omega_1 L=\dfrac{1}{\omega_1C}\)\(\Rightarrow \omega_1=\sqrt{\dfrac{0,64}{0,28}}.\omega_2\)
\(\Rightarrow f_1=\sqrt{\dfrac{0,64}{0,28}}.f_2=...\)
Bạn làm tiếp với TH2 nhé :)