HM
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 9 2016
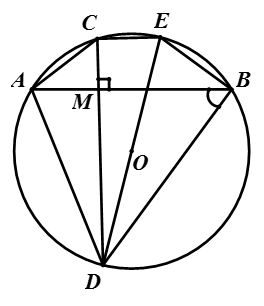
A B C D M E O
Gọi E là điểm đối xứng với C qua tâm O của đường tròn
Dễ dàng chứng minh được ABED là hình thang cân.
=> BD = AE
Ta có : \(MA^2+MB^2+MC^2+MD^2=\left(MA^2+MC^2\right)+\left(MB^2+MD^2\right)=AC^2+BD^2\)
\(=AC^2+AE^2=CE^2=\left(2R\right)^2=4R^2\) KHÔNG ĐỔI.
HT
0
H
24 tháng 3 2020
a) Xét ΔAMC và ΔDMB có:
góc ACD = góc ABD (góc nội tiếp cùng chắn cung AD)
góc AMC = góc BMD = 90o (gt)
=> ΔAMC ∼ ΔDMB (g.g)
=> MA/MD = MC/MB => MA.MB = MC.MD
b) Vì góc DCE = 90 độ (góc nội tiếp chắn nửa đường tròn)
=> CD ⊥ CE
Mà CD ⊥ AB (gt)
=> AB // CE
=> Tứ giác ABEC là hình thang (1).
Mặt khác: CE và AB là hai dây song song của đường tròn (O) chắn hai cung AC và BE nên \(\stackrel\frown{AC}=\stackrel\frown{BE}\)
=> \(sd\stackrel\frown{AE}+sd\stackrel\frown{EC}=sd\stackrel\frown{BC}+sd\stackrel\frown{EC}\)
=>\(sd\stackrel\frown{AE}=sd\stackrel\frown{BC}\) => \(\widehat{ABE}=\widehat{CAB}\) (2)
Từ (1) và (2) => đpcm
c, Vì \(\stackrel\frown{AC}=\stackrel\frown{BE}\Rightarrow AC=BE\)
Ta có: góc DAE = 90 độ (góc nội tiếp chắn nửa đường tròn)
Ta có: \(MA^2+MB^2+MC^2+MD^2\)
\(=\left(MA^2+MD^2\right)+\left(MB^2+MC^2\right)\) (áp dụng pytago vào t/g MAD và MBC)
\(=AD^2+BC^2=AD^2+AE^2=DE^2=4R^2\) không đổi (pytago)
SL
0
12 tháng 9 2021
Từ M kẻ ME vuông góc với AB,MF vuông góc với AC.
Ta có ΔEBM vuông cân tại E, ΔFMC vuông cân tại F và AEMF là hình chữ nhật.
Áp dụng định lý Pytago vào các tam giác EBM,FMC,AEF ta có:
BM^2 = EM^2 + BE^2 = 2.ME^2 ; MC^2 = 2.FM^2 ⇒ BM^2 + MC^2 = 2.(ME^2 + MF^2) (1)
Mà AM^2 = EF^2 = ME^2 + MF^2 (2)
Từ (1),(2) ta được 2AM^2 = MB^2 + MC^2
PT
1