Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

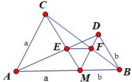
Vì các tam giác AMC và BMD đều nên B M D ^ = M A C ^ = 90 ° (vì hai góc ở vị trí đồng vị) => MD // AC
Vì MD // AC nên theo hệ quả định lý Talet cho hai tam giác DEM và AEC ta có M E E C = M D A C = b a
Suy ra
M E E C = b a ⇒ M E M E + E C = b b + a ⇒ M E a = b b + a ⇒ M E = a b b + a
Tương tự MF = b a a + b
Vậy M E = M F = a b b + a
Đáp án: B

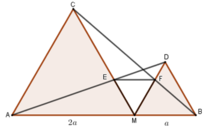
Đặt MB = a => MA = 2a
Vì các tam giác AMC và BMD đều nên B M D ^ = M A C ^ = 60 ° (hai góc ở vị trí đồng vị) => MD // AC
Vì MD // AC nên theo hệ quả định lý Talet cho hai tam giác DEM và AEC ta có
M E E C = M D A C = M B M A = 1 2
Suy ra:
M E E C = b a ⇒ M E M E + E C = 1 1 + 2 = 1 3 ⇒ M E 2 a = 1 3 ⇒ M E = 2 a 3
Tương tự MF = 2 a 3
Vậy M E = M F = 2 a 3
Đáp án: B

Đáp án:
a) EFIK là hình thang cân.
b) FK = 1/2 MD.
Giải thích các bước giải:
Ta có: EF là đường TB của tam giác MBC => EF // BC.
IK là đường TB của tam giác ABD => IK // AB
=> EF // IK => EFIK là hình thang.
Ta có: Gọi N là trung điểm của BC ta có EF // NC, EF = NC => EFNC là hình bình hành => FN // EC
IN là đường TB của tam giác BCD => IN // BD.
Mà BD // MC (góc MCA = góc DBC = 60 độ, mà 2 góc này ở vị trí đồng vị).
=> IN // MC
=> F, I, N thẳng hàng.
=> FI // MC.
Mà IK // AC => góc FIK = góc MCA = 60 độ.
CMTT ta có KE // MA. Mà KI // AC
=> góc EKI = góc MAC = 60 độ.
=> EFIK là hình thang cân.
=> EI = KF.
Mà EI là đường TB của tam giác CDM => EI = ½ MD
=> KF = ½ MD.



Từ câu trước ta có ME = MF => ΔEMF cân tại M
Ta có A M C ^ + E M F ^ + D M B ^ = 180 ° mà C M A ^ = D M B ^ = 30 ° (tính chất tam giác đều)
Nên:
E M F ^ = 180 ° - M N A ^ - D M B ^ = 180 ° - 60 ° - 60 °
Từ đó MEF là tam giác cân có một góc bằng 60 ° nên nó là tam giác đều
Đáp án: A