
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

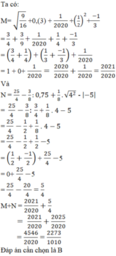

Bài 2:
1: \(5^n+5^{n+2}=650\)
\(\Leftrightarrow5^n\cdot26=650\)
\(\Leftrightarrow5^n=25\)
hay x=2
2: \(32^{-n}\cdot16^n=1024\)
\(\Leftrightarrow\dfrac{1}{32^n}\cdot16^n=1024\)
\(\Leftrightarrow\left(\dfrac{1}{2}\right)^n=1024\)
hay n=-10
13: \(9\cdot27^n=3^5\)
\(\Leftrightarrow3^{3n}=3^5:3^2=3^3\)
=>3n=3
hay n=1

3/ ta để ý thấy ở số mũ sẽ có thừa số 1000-103=0
nên số mũ chắc chắn bằng 0
mà số nào mũ 0 cũng bằng 1 nên A=1
5/ vì |2/3x-1/6|> hoặc = 0
nên A nhỏ nhất khi |2/3x-6|=0
=>A=-1/3
6/ =>14x=10y=>x=10/14y
23x:2y=23x-y=256=28
=>3x-y=8
=>3.10/4y-y=8
=>6,5y=8
=>y=16/13
=>x=10/14y=10/14.16/13=80/91
8/106-57=56.26-56.5=56(26-5)=59.56
có chứa thừa số 59 nên chia hết 59
4/ tính x
sau đó thế vào tinh y,z

Bài 1:
c) \(\dfrac{5^4.20^4}{25^5.4^5}=\dfrac{5^4.4^4.5^4}{5^{10}.4^5}=\dfrac{5^8.4^4}{5^8.5^2.4^4.4}=\dfrac{1}{25.4}=\dfrac{1}{100}\)
Bài 2: a) \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{5}\right)^{2004}\ge0\forall x\\\left(y+0,4\right)^{100}\ge0\forall y\\\left(z-3\right)^{678}\ge0\forall z\end{matrix}\right.\) \(\Rightarrow\left(x-\dfrac{1}{5}\right)^{2004}+\left(y+0,4\right)^{100}+\left(z-3\right)^{678}\ge0\forall x,y,z\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{5}\right)^{2004}=0\\\left(y+0,4\right)^{100}=0\\\left(z-3\right)^{678}=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}\\y=-\dfrac{2}{5}\\z=3\end{matrix}\right.\)
Vậy ...
Bài 3: \(M=\dfrac{8^{10}+4^{10}}{8^4+4^{11}}=\dfrac{\left(2^3\right)^{10}+\left(2^2\right)^{10}}{\left(2^3\right)^4+\left(2^2\right)^{11}}=\dfrac{2^{30}+2^{20}}{2^{12}+2^{22}}\)
\(=\dfrac{2^{20}\left(2^{10}+1\right)}{2^{12}\left(2^{10}+1\right)}=\dfrac{2^{20}}{2^{12}}=2^8=256.\)
Vậy \(M=256.\)
Mấy bài kia dễ tự làm.
\(3)\)
\(\dfrac{8^{10}+4^{10}}{8^4+4^{11}}=\dfrac{\left(2^3\right)^{10}+\left(2^2\right)^{10}}{\left(2^3\right)^4+\left(2^2\right)^{11}}=\dfrac{2^{30}+2^{20}}{2^{12}+2^{22}}=\dfrac{2^{20}\left(2^{10}+1\right)}{2^{12}\left(2^{10}+1\right)}=\dfrac{2^{20}}{2^{12}}=2^8=256\)\(4)\)
\(2^{24}=\left(2^6\right)^4=64^4;3^{16}=\left(3^4\right)^4=81^4\)
\(\Leftrightarrow2^{24}< 3^{16}\)

\(a)\dfrac{1}{4}-\dfrac{3}{4}:\left(\dfrac{-5}{8}\right)\)
\(=\dfrac{1}{4}-\dfrac{3}{4}.\dfrac{-8}{5}\)
\(=\dfrac{1}{4}-\dfrac{-6}{5}\)
\(=\dfrac{5}{20}+\dfrac{24}{20}\)
\(=\dfrac{29}{20}\)
\(b)3-\left(\dfrac{-6}{7}\right)^0+\sqrt{\dfrac{1}{16}}:2\)
\(=3-1+\sqrt{\left(\dfrac{1}{4}\right)^2}:2\)
\(=2+\dfrac{1}{4}.\dfrac{1}{2}\)
\(=\dfrac{16}{8}+\dfrac{1}{8}\)
\(=\dfrac{17}{8}\)
\(c)\dfrac{9^5.2^6}{4^3.3^8}=\dfrac{\left(3^2\right)^5.2^6}{\left(2^2\right)^3.3^8}=\dfrac{3^{10}.2^6}{2^6.3^8}=3^2=9\)

1) Theo định nghĩa về căn bậc 2 số học thì đáp án là \(\sqrt{5^2}; \sqrt{(-5)^2}\)
2) Tập $Q$ là tập những số thực biểu diễn được dưới dạng \(\frac{a}{b}\) (a,b tự nhiên, $b$ khác $0$), tập $I$ là tập những số thực không biểu diễn được dạng như trên.
\(0,15=\frac{3}{20}\in\mathbb{Q}\) , A sai.
$\sqrt{2}$ là một số vô tỉ (tính chất quen thuộc), B sai.
$C$ hiển nhiên đúng, theo định nghĩa.
Do đó áp án đúng là C.
3)
a) \(-\sqrt{x}=(-7)^2=49\)
\(\Rightarrow \sqrt{x}=-49\) (vô lý, vì căn bậc 2 số học của một số là một số không âm , trong khi đó $-49$ âm)
Do đó pt vô nghiệm.
b) \(\sqrt{x+1}+2=0\Rightarrow \sqrt{x+1}=-2<0\)
Điều trên hoàn toàn vô lý do căn bậc 2 số học là một số không âm
Vậy pt vô nghiệm.
c) \(5\sqrt{x+1}+2=0\Rightarrow \sqrt{x+1}=\frac{-2}{5}<0\)
Điều trên hoàn toàn vô lý do căn bậc 2 số học là một số không âm
Vậy pt vô nghiệm.
d) \(\sqrt{2x-1}=29\Rightarrow 2x-1=29^2=841\Rightarrow x=\frac{841+1}{2}=421\)
e)\(x^2=0\Rightarrow x=\pm \sqrt{0}=0\)
g) \((x-1)^2=1\frac{9}{16}=\frac{25}{16}\)
\(\Rightarrow x-1=\pm \sqrt{\frac{25}{16}}=\pm \frac{5}{4}\)
\(\Rightarrow \left[\begin{matrix} x=\frac{9}{4}\\ x=\frac{-1}{4}\end{matrix}\right.\)
h) \(\sqrt{3-2x}=1\Rightarrow 3-2x=1^2=1\Rightarrow x=\frac{3-1}{2}=1\)
f) \(\sqrt{x}-x=0\Rightarrow \sqrt{x}=x\Rightarrow x=x^2\)
\(\Rightarrow x(1-x)=0\Rightarrow \left[\begin{matrix} x=0\\ x=1\end{matrix}\right.\)

1)Ta có ; x:y:z=3:4:5 =>\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\Rightarrow\frac{x^2}{3^2}=\frac{y^3}{4^3}=\frac{z^2}{5^2}\Rightarrow\frac{2x^2}{18}=\frac{2y^3}{128}=\frac{3z^2}{75}\)
áp đụng tính chất của dãy tỉ số bằng nhau và 2x2+2y3-3z2=-100
Ta được : \(\frac{2x^2}{18}=\frac{2y^3}{128}=\frac{3z^2}{75}=\frac{2x^2+2y^3-3z^2}{18+128-75}=\frac{-100}{71}\)
CÒN LẠI BẠN TỰ TÍNH NHÉ
2)
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a^1-1}{9}=\frac{a^2+2}{8}=...=\frac{a^9-9}{1}\)
=\(\frac{a^1-1+a^2-2+...+a^9-9}{9+8+...+1}=\frac{\left(a^1+a^2+...+a^9\right)-\left(9+8+...+1\right)}{9+8+...+1}\)
=\(\frac{90-45}{45}=\frac{45}{45}=1\)
suy ra:\(\frac{a^1-1}{9}=1\Rightarrow a^1=10\)tương tự ta có: a1=a2=...=a9=10