


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




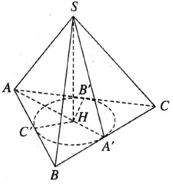
Kẻ SH ⊥ (ABC) và HA’, HB’ , HC’ lần lượt vuông góc với BC, CA, AB. Theo định lí ba đường vuông góc ta có SA′ ⊥ BC, SB′ ⊥ CA, SC′ ⊥ AB
Từ đó suy ra ∠ SA′H = ∠ SB′H = ∠ SC′H = 60 ° .
Do đó các tam giác vuông SHA’ , SHB’ , SHC’ bằng nhau. Từ đó suy ra HA’ = HB’ = HC’ . Vậy H là tâm đường tròn nội tiếp tam giác ABC. Do tam giác cân ở A nên AH vừa là đường phân giác , vừa là đường cao, vừa là đường trung tuyến. Từ đó suy ra A, H, A’ thẳng hàng và A’ là trung điểm của BC.
Do đó, AA ' 2 = AB 2 - BA ' 2 = 25 a 2 - 9 a 2 = 16 a 2
Vậy AA’ = 4a
Gọi p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp của nó.
Khi đó SABC = 6a.4a/2 = 12a2 = pr = 8ar
Từ đó suy ra r = 3a/2
Do đó
![]()
Thể tích khối chóp là:
![]()

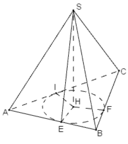

ta có công thức S=p.r, ta có r = S P = 2 a 6 3
=> SH=EH.tan S E H ^ = r . tan 60 o = 2 a 6 3 3 = 2 a 2


Đáp án B
Gọi H là chân đường vuông góc hạ từ S xuống mặt phẳng (ABC).
Kẻ HM, HN, HP lần lượt vuông góc với AB, BC, CA trong mặt phẳng (ABC).
Sử dụng tính chất ba đường cvuoong góc ta dễ chứng minh được SM, SN, SP lần lượt vuông góc với AB, BC, CA


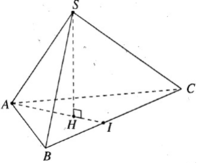
Kẻ SH ⊥ (ABC). Đường thẳng AH cắt BC tại I.
Do S.ABC là hình chóp tam giác đều nên H là trọng tâm của ΔABC.
Do đó
![]()
![]()
Thể tích khối chóp S.ABC là:
![]()