
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 4/3 x 2/5 - 3/4 x 2/5
= (4/3 - 3/4) x 2/5
= 7/12 x 2/5
= 7/30
b) 3 x ( -4/30)2 - 7/3
= 3 x 4/225 - 7/3
= 4/75 - 7/3
= -2,28
c) -0,8 x 1/9/25 - 4/5 x 64/25
= -4/5 x 1,36 - 4/5 x 2,56
= -4/5 x (1,36 - 2,56)
= -4/5 x (-1,2)
= 0,96

II. Trắc Nghiệm
Câu 1: Cho x = | x| kết quả nào đúng sau đây
a. x = 0
b. x = 1
c. x > 0
d. x ≥ 0
Câu 2: Trong các phân số sau, phân số nào biểu diễn số hữu tỷ 2/-5?
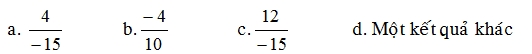
=> Chọn B
Câu 3: 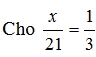 giá trị của x bằng bao nhiêu?
giá trị của x bằng bao nhiêu?
a. 63
b. 1/7
c. 7
d. 0,7
Câu 4: 76 + 75 – 74 chia hết cho:
a. 5
b.7
c.11
d. Cả 3 số trên
Câu 5: Kết quả nào sau đây là đúng ?
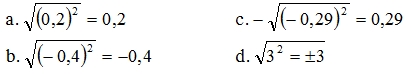
=> Chọn A
Câu 6: Câu nào trong các câu sau đây SAI

I. TRẮC NGHIỆM KHÁCH QUAN (3đ)
Khoanh tròn vào đáp án đúng trong các câu sau:
Câu 1: Trong các câu sau, câu nào sai
A. Nếu a là số thực thì a là số hữu tỉ hoặc số vô tỉ
B. Nếu b là số vô tỉ thì b viết được dưới dạng số thập phân vô hạn không tuần hoàn
C. Nếu c là số vô tỉ thì c cũng là số thực
D. Nếu c là số thực thì c cũng là số vô tỉ
Câu 2: Kết qủa của phép tính 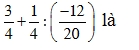
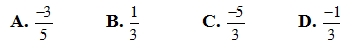
=> Chọn B
Câu 3: Kết qủa của phép tính 36 . 32 =
A. 98
B. 912
C. 38
D. 312
=> 1152
Câu 4: Từ đẳng thức a.d = b.c có thể suy ra tỉ lệ thức nào sau đây:
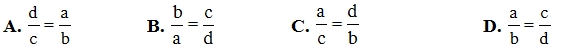
=> Chọn D
Câu 5: Viết số thập phân hữu hạn dưới dạng phân số tối giản :
![]()
=> Chọn A
Câu 6: Nếu √x = 3 thì x =
A. 3
B. 9
C. -9
D. ±9
II. TRẮC NGHIỆM TỰ LUẬN (7đ)
Bài 1 (1,5đ) Tính:
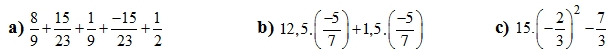
\(=\left(\frac{8}{9}+\frac{1}{9}\right)+\left(\frac{15}{23}-\frac{15}{13}\right)+\frac{1}{2}\) \(=\left(-\frac{5}{7}\right)\times\left(12,5+1,5\right)\) \(=15\times\frac{4}{9}-\frac{7}{3}\)
\(=\frac{9}{9}+0+0,5\) \(=\left(-\frac{5}{7}\right)\times14\) \(=\frac{20}{3}-\frac{7}{3}\)
\(=1+0,5\) \(=-10\) \(=\frac{13}{3}\)
\(=1,5\)
Bài 2 (2đ): Ba lớp 8A, 8B, 8C trồng được 180 cây . Tính số cây trồng được của mỗi lớp, biết rằng số cây trồng được của mỗi lớp lần lượt tỉ lệ với 4 : 6 : 8
Gọi số cây trồng được của lớp 8A, 8B, 8C theo thứ tự là a, b và c.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{4}=\frac{b}{6}=\frac{c}{8}=\frac{a+b+c}{4+6+8}=\frac{180}{18}=10\)
\(\left[\begin{array}{nghiempt}\frac{a}{4}=10\\\frac{b}{6}=10\\\frac{c}{8}=10\end{array}\right.\)
\(\left[\begin{array}{nghiempt}a=10\times4\\b=10\times6\\c=10\times8\end{array}\right.\)
\(\left[\begin{array}{nghiempt}a=40\\b=60\\c=80\end{array}\right.\)
Vậy số cây trồng được của lớp 8A, 8B, 8C theo thứ tự là 40 cây, 60 cây và 80 cây.
Bài 3 (1,5đ): Tìm x, biết
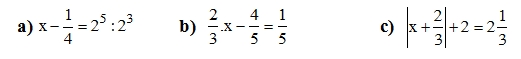
\(x-\frac{1}{4}=2^2\) \(\frac{2}{3}x=\frac{1}{5}+\frac{4}{5}\) \(\left|x+\frac{2}{3}\right|+\frac{6}{3}=\frac{7}{3}\)
\(x-\frac{1}{4}=4\) \(\frac{2}{3}x=\frac{5}{5}\) \(\left|x+\frac{2}{3}\right|=\frac{9}{3}-\frac{7}{3}\)
\(x=\frac{16}{4}+\frac{1}{4}\) \(x=1\div\frac{2}{3}\) \(\left|x+\frac{2}{3}\right|=\frac{2}{3}\)
\(x=\frac{17}{4}\) \(x=1\times\frac{3}{2}\) \(x+\frac{2}{3}=\pm\frac{2}{3}\)
\(x=\frac{3}{2}\) \(\left[\begin{array}{nghiempt}x+\frac{2}{3}=\frac{2}{3}\\x+\frac{2}{3}=-\frac{2}{3}\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=\frac{2}{3}-\frac{2}{3}\\x=-\frac{2}{3}-\frac{2}{3}\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=0\\x=-\frac{4}{3}\end{array}\right.\)
Bài 4 (1đ): So sánh các số sau: 2550 và 2300
2550 > 2300
Bài 5 (1đ): Cho N = 9/ (√x -5). Tìm x ∈ Z để N có giá trị nguyên.
\(N\in Z\)
\(\Leftrightarrow9⋮\sqrt{x}-5\)
\(\Leftrightarrow\sqrt{x}-5\in\text{Ư}\left(9\right)=\left\{-9;-3;-1;1;3;9\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{-4;2;4;6;8;14\right\}\)
\(\Leftrightarrow x\in\left\{\sqrt{-4};\sqrt{2};\sqrt{4};\sqrt{6};\sqrt{8};\sqrt{14}\right\}\)
mà \(x\in Z\)
=> x = 2

Gọi D là giao điểm của AC và BY
GT: Ax // By ; \(\widehat{xAC}\) = 130o ; \(\widehat{C}\) = 90o ; AC \(\cap\) By = D
KL: \(\widehat{CBy}\) = ?
Vì Ax // By (gt) nên ta có:
\(\widehat{A}\) = \(\widehat{D}\) = 120o ( 2 góc đồng vị)
Mà \(\widehat{D}\) là góc ngoài tại đỉnh D của ΔBCD nên:
\(\Rightarrow\) \(\widehat{CBy}\) + \(\widehat{C}\) = \(\widehat{D}\)
hay \(\widehat{CBy}\) + 90o = 120o
\(\Rightarrow\) \(\widehat{CBy}\) = 120o - 90o = 30o
Vậy \(\widehat{CBy}\) = 30o
vì A //B (gt)
=> xAc = BOA ( 2 góc so le trong)
mà xAC= 120*(gt)
=> BOA= 120*
ta có : C + B = BOA ( định nghĩa góc ngoài của tam giác )
mà BOA = 120* ( cm trên) , C= 90*( gt)
=> B = 120*-90*=30*
hết rồi nha bn ( có j ký hiệu góc và độ mik ko biết đánh nên bn tự hiểu nha )![]()

ĐỀ 1
A/ PHẦN TRẮC NGHIỆM (3 điểm)
Khoanh tròn chữ cái đầu câu trả lời đúng nhất:
Câu 1: Tính 53. 52 =
A: 55
B: 56
C: 255
D: 256
=> 2756
Câu 2: Tính 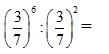

=> Chọn A
Câu 3: Điền số thích hợp vào ô trống [(- 0,2 )6 ]5 = (-0,2) ….
A/ 11
B/ 30
C/ 56
D/ 65
Câu 4: Kết quả nào sai?
![]()
=> Chọn D
Câu 5: |x | = 11 thì x bằng:
A/ 11
B/ – 11
C/ ± 11
D/ Cả A, B, C đều sai.
Câu 6: √t = 4 thì t bằng:
A/ 16
B/ ±16
C/ 8
D/ ±8

ĐỀ 2
I. PHẦN TRẮC NGHIỆM: (3 điểm)
Khoanh tròn chữ cái đứng trước câu trả lời đúng:
1. Trong các khẳng định sau, khẳng định sai là:
A. I ⊂ R
B. I ∪ Q = R
C. Q ⊂ I
D. Q ⊂ R
2. Kết quả của phép nhân (-0,5)3.(-0,5) bằng:
A. (-0,5)3
B. (-0,5)
C. (-0,5)2
D. (0,5)4
3. Giá trị của (-2/3) ³ bằng:

=> Chọn B
4. Nếu | x | = |-9 |thì:
A. x = 9 hoặc x = -9
B. x = 9
B. x = -9
D. Không có giá trị nào của x để thỏa mãn
5. Kết quả của phép tính 36.34. 32 bằng:
A. 2712
B. 312
C. 348
D. 2748
=> 39168
6. Kết quả của phép tính ![]()

Theo đề, ta có:
\(\dfrac{a+b-c}{3c}=\dfrac{b+c-a}{3a}=\dfrac{c+a-b}{3b}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a+b-c}{3c}=\dfrac{b+c-a}{3a}=\dfrac{c+a-b}{3b}=\dfrac{a+b-c+b+c-a+c+a-b}{3c+3a+3b}=\dfrac{a+b+c}{3c+3a+3b}\)
\(=\dfrac{a+b+c}{3.\left(a+b+c\right)}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{a+b-c}{3c}=\dfrac{1}{3}\Rightarrow a+b-c=\dfrac{3c}{3}=c\Rightarrow a+b=2c\)
và \(\dfrac{b+c-a}{3a}=\dfrac{1}{3}\Rightarrow b+c-a=\dfrac{3a}{3}=a\Rightarrow b+c=2a\)
và \(\dfrac{c+a-b}{3b}=\dfrac{1}{3}\Rightarrow c+a-b=\dfrac{3b}{3}=b\Rightarrow c+a=2b\)
\(\Rightarrow P=\left(1+\dfrac{b}{a}\right)\left(1+\dfrac{a}{c}\right)\left(1+\dfrac{c}{b}\right)=\left(\dfrac{a+b}{a}\right)\left(\dfrac{c+a}{c}\right)\left(\dfrac{b+c}{b}\right)\)
\(=\left(\dfrac{2c}{a}\right)\left(\dfrac{2b}{c}\right)\left(\dfrac{2c}{b}\right)=\dfrac{2c.2a.2b}{a.b.c}=8\)
Vậy P = 8


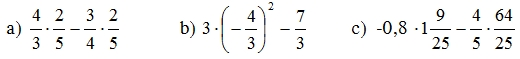
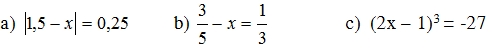

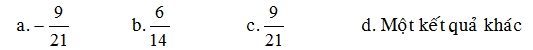
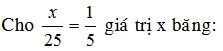

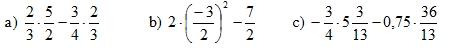



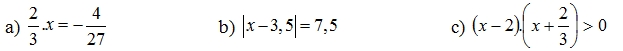

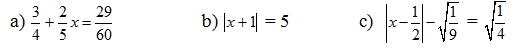


\(A=\dfrac{5n+1}{n+1}=\dfrac{5\left(n+1\right)-4}{n+1}\)
\(Để\) \(\dfrac{5n+1}{n+1}\in Z\Rightarrow4⋮n+1\)
\(\Rightarrow n+1\inƯ\left(4\right)=\left\{-1;-2;-4;1;2;4\right\}\)
\(n+1=-1\Rightarrow n=-2\)
\(n+1=-2\Rightarrow n=-3\)
\(n+1=-4\Rightarrow n=-5\)
\(n+1=1\Rightarrow n=0\)
\(n+1=2\Rightarrow n=1\)
\(n+1=4\Rightarrow n=3\)
0;1;3