Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

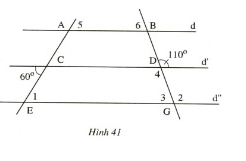
1) Tính góc ∠E1
Ta có d’//d” (gt)
⇒ ∠C = ∠E1 ( So le trong)
⇒ ∠E1 = 600 vì ∠C = 600
2) Tính ∠G3
Ta có d’//d”
⇒ ∠G2 = ∠D (Đồng vị)
⇒ ∠G1 = 1100
3) Tính ∠G3
Vì ∠G2 + ∠G3 = 1800 (kề bù)
⇒ ∠G3 = 700
4) Tính ∠D4
∠D4 = ∠D (Đối đỉnh)
⇒ ∠D4 = 1100
5) Tính ∠A5
Ta có d//d”
⇒ ∠A5 = ∠ E1 (Đồng vị)
⇒ ∠A5 = 600
6) Tính ∠B6
Ta có d//d”
⇒ ∠B6 = ∠G3 (Đồng vị)
⇒ ∠B6 = 700


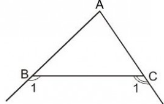
ta có tổng ba góc trong một tam giác bằng 1800
nên\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{A}=180^0-\left(\widehat{B}+\widehat{C}\right)\)
\(\Rightarrow\widehat{A}=180^0-\left(80^0+30^0\right)\)
\(\Rightarrow\widehat{A}=70^0\)
Do tia phân giác của góc A cắt BC ở D
Nên \(\Rightarrow\widehat{BAD}=\widehat{CAD}=70:2=35^0\)
Ta có :\(\widehat{B}+\widehat{BAD}+\widehat{ADB}=180^0\)
\(\Rightarrow\widehat{ADB}=180^0-\left(\widehat{B}+\widehat{BAD}\right)\)
\(\Rightarrow\widehat{ADB}=180^0-\left(80^0+35^0\right)\)
\(\Rightarrow\widehat{ADB}=65^0\)
\(\Rightarrow\widehat{ADC}=180^0-65^0=115^0\)
Vậy :\(\widehat{ADC}=115^0\)
\(\widehat{ADB}=65^0\)
tự vẽ hình nha

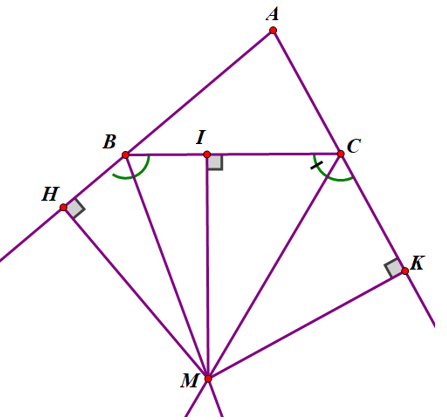
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).